Calculating Force on a Pin with Ropes and Tensions?

[warfreak131]

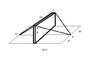
Homework Statement

A precast concrete wall is temporarily kept in its vertical position by ropes. Find the total force exerted on the pin at position A. The tensions in AB and AC are 420 lbs and 650 lbs.

The Attempt at a Solution

I'm not sure where to start, because I don't know whether or not the tension from DB to DC also counts towards the force on the pin at A. I am also not sure on what values to add. Like if I add vectors AB and AC, is the result at the same angle?

 

[tiny-tim]

… I don't know whether or not the tension from DB to DC also counts towards the force on the pin at A.

Hi warfreak131!

There's no force-at-a-distance … the only forces at A are the forces at A.

I am also not sure on what values to add. Like if I add vectors AB and AC, is the result at the same angle?

You add the force vectors, not the position vectors.

(All the angles are either equal or opposite, so yes you could take a short-cut for each component separately … but I wouldn't recommend it.)

 

[warfreak131]

Hi warfreak131!

There's no force-at-a-distance … the only forces at A are the forces at A.


You add the force vectors, not the position vectors.

(All the angles are either equal or opposite, so yes you could take a short-cut for each component separately … but I wouldn't recommend it.)

ok, but DC, and DB are pulling on the wall too, so wouldn't that put extra tension in the cables AB and AC and cause the pin to experience a greater force?

 

[tiny-tim]

ok, but DC, and DB are pulling on the wall too, so wouldn't that put extra tension in the cables AB and AC and cause the pin to experience a greater force?

ah, but that's taken account of in the question …

The tensions in AB and AC are 420 lbs and 650 lbs.

… it may well put extra tension in AB and AC, but you've been given figures that include that!

 

[warfreak131]

ah, but that's taken account of in the question …


… it may well put extra tension in AB and AC, but you've been given figures that include that!

very true sir... very true,

so should i just find the angles that the cables make with the fore and background edges, and then add the force vectors?

 

[tiny-tim]

Yes, except that you don't actually need to find the angles, you can get the cosines just by using the coordinates, and dividing by the hypotenuse.

 

[warfreak131]

Yes, except that you don't actually need to find the angles, you can get the cosines just by using the coordinates, and dividing by the hypotenuse.

ok, thanks a bunch