Calculating Hydrostatic Force on Dam Plug

[rdn98]

Picture is included.

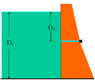
You are working as a summer intern for the Illinois Department of Natural Resources (DNR) and are assigned to some initial work on water resources project. The department will be overseeing the construction of a dam to create a large fresh water lake that will be approximately 18 meters deep. A horizontal pipe 1.2 meters long and 5 cm in diameter will pass through the dam at a depth of 6 meters to allow for release of the water in emergencies and for sampling. In normal situations, a plug will secure the pipe opening.
--------------------------------------------------------------------------------
(a) What will be the hydrostatic force on the plug?

How do I setup the equation for a hydrostaic force? I've tried various FBD, but none is getting me anywhere.

Ok, I know that at the same horizontal level of the pipe, the pressure is constant at that depth.

FBD of the plug shows a mg down, a bouyant force pointing to the right, and normal force up from the dam, and a foce pushing the plug down from the dam also.

So the forces in y direction cancel out. And I assume that the hydrostatic force would be the same thing as the bouyant force for this question? I am stuck and need help badly.

 

[Doc Al]

Originally posted by rdn98
... I am stuck and need help badly.

I think you are making too much out of a simple problem. The hydrostatic force on the plug is just the force due to the water pressure. Find the pressure at depth D₂ and then calculate the force. (Ignore atmospheric pressure--since it's the same on both sides of the plug.)

 

[M98Ranger]

To calculate the hydrostatic force on the dam plug, you will need to use the equation F = ρghA, where F is the hydrostatic force, ρ is the density of the fluid (in this case, water), g is the acceleration due to gravity (9.8 m/s^2), h is the depth of the fluid, and A is the area of the plug.

In this scenario, the depth of the water is given as 6 meters and the area of the plug can be calculated using the formula for the area of a circle (A = πr^2). The radius of the plug can be calculated by dividing the diameter (5 cm) by 2 and converting it to meters (0.025 meters).

So, the area of the plug would be A = π(0.025)^2 = 0.00196 m^2.

Now, plugging in all the values into the equation, we get:

F = (1000 kg/m^3)(9.8 m/s^2)(6 m)(0.00196 m^2) = 115.68 N

Therefore, the hydrostatic force on the dam plug is approximately 115.68 N. This means that in order to keep the plug in place, there needs to be a force of at least 115.68 N pushing against it. Any less force and the plug will be pushed out by the pressure of the water.

Remember, the hydrostatic force is equal to the buoyant force in this scenario because the plug is completely submerged in water. The buoyant force is the force exerted by a fluid on an object that is partially or fully submerged in it.

I hope this helps you understand how to calculate the hydrostatic force on a dam plug. If you have any further questions, don't hesitate to ask. Good luck with your internship!