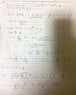Calculating Impedance and Effective Power in a Complex Circuit

[MissP.25_5]

Hi, can you please check my answer? I am not confident because the power consumption seems too small.
By the way, we don't use calculator at all so we don't have to calculate to the exact value. For example, if there is "pi", we can just leave it as it is, without converting it into 3.142. Also, if there is square root of 2, just leave it as square root of 2, no need to calculate it as 1.41.

Ok, here is the question:
v1(t) and v2(t) are given as written in the question.

1) Find the value of impedance Z.
2) Find the power consumption (effective power) of the entire circuit.

 

[gneill]

Check your calculation for Z2. There's a resistance and an inductor in parallel so you should end up with a complex result with both real and imaginary components. Note that you can read the angular frequency $(\omega )$ from the voltage expressions.

 

[MissP.25_5]

Check your calculation for Z2. There's a resistance and an inductor in parallel so you should end up with a complex result with both real and imaginary components. Note that you can read the angular frequency $(\omega )$ from the voltage expressions.

Oh yes, that is a careless mistake! Here I have corrected it. Is this new answer ok? I am still not sure about the effective power, though.

 

[gneill]

The parallel impedance looks fine now.

I suggest, since you will be calculating power, that you convert the given peak voltages to RMS phasors before proceeding with further calculations. You could do the calculations with peak values, but you would have to be careful with the power calculation. Using RMS makes things straightforward throughout, even though you'll by carrying along a few √2's.

What will be your RMS value for I?

 

[MissP.25_5]

The parallel impedance looks fine now.

I suggest, since you will be calculating power, that you convert the given peak voltages to RMS phasors before proceeding with further calculations. You could do the calculations with peak values, but you would have to be careful with the power calculation. Using RMS makes things straightforward throughout, even though you'll by carrying along a few √2's.

What will be your RMS value for I?

Uhmmm...how do I find RMS? Is this the formula : Irms = I/√2

 

[gneill]

Uhmmm...how do I find RMS? Is this the formula : Irms = I/√2

That would work, if I is a peak value. Or, begin with RMS values for the voltages before calculating the current. You'll be using RMS values for both voltage and current in your power calculations.

 

[MissP.25_5]

That would work, if I is a peak value. Or, begin with RMS values for the voltages before calculating the current. You'll be using RMS values for both voltage and current in your power calculations.

I used RMS values for the voltages. Now, is this ok?

 

[gneill]

To find RMS values, divide peak by √2. It looks like you've multiplied by √2 instead.

 

[MissP.25_5]

To find RMS values, divide peak by √2. It looks like you've multiplied by √2 instead.

Oh yes, another careless one! OK, corrected it. So now is this correct?

 

[gneill]

Your V2 phasor doesn't look right. It's peak magnitude is 1, so it's RMS magnitude should be 1/√2. The angle stays the same at 90°, so the phasor will be j/√2.

To calculate the power, note that if know both V1 and V2 you can find the voltage of the source (KVL), call it E . You already know the current phasor I. The complex power is just p = EI*, where I* is the complex conjugate of the current. The real part of the result is the real (effective) power delivered by the source and absorbed by the circuit.

 

[MissP.25_5]

Your V2 phasor doesn't look right. It's peak magnitude is 1, so it's RMS magnitude should be 1/√2. The angle stays the same at 90°, so the phasor will be j/√2.

To calculate the power, note that if know both V1 and V2 you can find the voltage of the source (KVL), call it E . You already know the current phasor I. The complex power is just p = EI*, where I* is the complex conjugate of the current. The real part of the result is the real (effective) power delivered by the source and absorbed by the circuit.

I tried to find the effective power in 2 different ways and I got two different answers. Can you explain to me why? I think the answer is 1/2, though.

 

[gneill]

I tried to find the effective power in 2 different ways and I got two different answers. Can you explain to me why? I think the answer is 1/2, though.

The first working is fine. Yes, the answer for effective power should be 1/2 W.

The second one goes wrong when you take the magnitude of E to use in the equation p = EI*. Use the complex value of E there. After multiplying out EI*, extract the real component of the result.

 

[MissP.25_5]

The first working is fine. Yes, the answer for effective power should be 1/2 W.

The second one goes wrong when you take the magnitude of E to use in the equation p = EI*. Use the complex value of E there. After multiplying out EI*, extract the real component of the result.

I used the complex value of E and complex value of I and the result I got is 0.

 

[gneill]

I used the complex value of E and complex value of I and the result I got is 0.

Your values for E and I are:
$$E = \left(\sqrt{2} + \frac{1}{\sqrt{2}} j \right) V = \sqrt{2}\left(1 + \frac{1}{2} j \right) V$$
$$I = \left( \frac{1}{4\sqrt{2}} + \frac{1}{2\sqrt{2}} j \right) A = \sqrt{2}\left( \frac{1}{8} + \frac{1}{4} j \right) A$$
Thus the complex power is given by
$$p = E I^* = \sqrt{2}\left(1 + \frac{1}{2} j \right) \sqrt{2}\left( \frac{1}{8} - \frac{1}{4} j \right) W = 2 \left(1 + \frac{1}{2} j \right) \left( \frac{1}{8} - \frac{1}{4} j \right) W $$

Note the sign change of the complex component of the current in order to form I*, the complex conjugate.

Carry out the multiplication and I think you'll find that effective power (real component of the complex power) is the same as for your other method.

 

[MissP.25_5]

Your values for E and I are:
$$E = \left(\sqrt{2} + \frac{1}{\sqrt{2}} j \right) V = \sqrt{2}\left(1 + \frac{1}{2} j \right) V$$
$$I = \left( \frac{1}{4\sqrt{2}} + \frac{1}{2\sqrt{2}} j \right) A = \sqrt{2}\left( \frac{1}{8} + \frac{1}{4} j \right) A$$
Thus the complex power is given by
$$p = E I^* = \sqrt{2}\left(1 + \frac{1}{2} j \right) \sqrt{2}\left( \frac{1}{8} - \frac{1}{4} j \right) W = 2 \left(1 + \frac{1}{2} j \right) \left( \frac{1}{8} - \frac{1}{4} j \right) W $$

Note the sign change of the complex component of the current in order to form I*, the complex conjugate.

Carry out the multiplication and I think you'll find that effective power (real component of the complex power) is the same as for your other method.

Why did you change the sign in I, j/4 to -j/4? Is it ok to do that?

 

[gneill]

Why did you change the sign in I, j/4 to -j/4? Is it ok to do that?

Not only is it okay, but it's required The complex power (real power + reactive power) is given by P = EI*, where I* is the complex conjugate of the current I. The complex conjugate is obtained by changing the sign of the imaginary term.

By finding power in this way you can do all the work from start to finish with complex math and you don't need to worry about remembering how to deal with power factors.

 

[MissP.25_5]

Not only is it okay, but it's required The complex power (real power + reactive power) is given by P = EI*, where I* is the complex conjugate of the current I. The complex conjugate is obtained by changing the sign of the imaginary term.

By finding power in this way you can do all the work from start to finish with complex math and you don't need to worry about remembering how to deal with power factors.

Oh, yes! Now I remember "complex conjugate". Thanks!