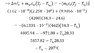Calculating initial temperature of iron block submerged into water

Click For Summary
SUMMARY

The discussion centers on calculating the initial temperature of an iron block submerged in water, with participants debating the accuracy of their results. One participant calculated the initial temperature as 207 degrees Celsius, while another obtained a significantly higher value, indicating a potential error in calculations. Key factors influencing the results include the specific heat capacity of iron (0.462 vs. 0.4605) and the mass of water (99.866 grams). The importance of significant figures and correct values for specific heat is emphasized throughout the conversation.

PREREQUISITES
  • Understanding of thermodynamics principles, specifically heat transfer.
  • Familiarity with specific heat capacity calculations.
  • Knowledge of significant figures in scientific measurements.
  • Proficiency in using equations for thermal equilibrium.
NEXT STEPS
  • Review the calculation of specific heat capacity for various materials.
  • Learn about thermal equilibrium and its applications in calorimetry.
  • Investigate the effects of significant figures on scientific calculations.
  • Explore the use of precise measurement tools for mass and temperature.
USEFUL FOR

Students in physics or engineering, educators teaching thermodynamics, and professionals involved in material science or thermal analysis will benefit from this discussion.

ayans2495
Messages
58
Reaction score
2
Homework Statement
A heated block of iron at temperature Ti with a mass of 61.331g is submerged into a beaker of water which has a mass of 200.562g and an inital temperature of 24.6 degrees Celsius. Once the iron is immersed into the water, 0.362 grams of the water evaporates. What is the initial temperature Ti of the iron block such that the final equilibrium temperature Tf is 34.3 degrees celsius?
Relevant Equations
Q=ml
Q=mcΔT Note: Δm=0.632
1614152916714.png
 
Physics news on Phys.org
Is my solution correct? If not, may you please advise me on how to change it?
 
Also, Δm actually equals 0.362. I made an error there.
 
Since your sign convention is unstated, it is hard to be sure whether your signs are correct. What numerical answer do you get?

(Quoting the masses to five and six figures when temperatures are only given to three is bizarre. Are you sure you have copied that correctly?)
 
I got that the initial temperature is 207 degrees Celsius as it was heated using a bunsen burner.
 
ayans2495 said:
I got that the initial temperature is 207 degrees Celsius as it was heated using a bunsen burner.
I get a considerably higher number. Please post the details of your working.
 
haruspex said:
I get a considerably higher number. Please post the details of your working.
I simply inputted the values provided into the equation I derived and solved for TiI. The sign convention of Q3 I believe is negative as if I were to make it positive I would end up with a negative result.
 
ayans2495 said:
I simply inputted the values provided into the equation I derived and solved for TiI.
Yes, but I did the same and get a rather different number, so one of us has an error. Please post the equation with all the numbers filled in.
 
haruspex said:
Yes, but I did the same and get a rather different number, so one of us has an error. Please post the equation with all the numbers filled in.
Perhaps I didn't round to the correct significant figures. When you asked whether or not I measured these correctly, the scale I used to measure these masses gave them in 4 to 5 s.f, but the thermometer in 3.May you please show me what values should be? I just posted my solution below.
 

Attachments

  • 1614236235925.png
    1614236235925.png
    7.2 KB · Views: 185
  • #10
ayans2495 said:
Perhaps I didn't round to the correct significant figures. When you asked whether or not I measured these correctly, the scale I used to measure these masses gave them in 4 to 5 s.f, but the thermometer in 3.May you please show me what values should be? I just posted my solution below.
Where does the 9.9866 figure come from? You gave the water mass as 200.562g.
Given the precision elsewhere, you should use 4186, not 4200.
 
  • #11
haruspex said:
Where does the 9.9866 figure come from? You gave the water mass as 200.562g.
Given the precision elsewhere, you should use 4186, not 4200.

Sorry the actual mass of the water is 99.866 grams. I will be sure to use 4186.
 

Similar threads

Final temperature for two blocks of iron placed in contact
  • · Replies 4 ·
Replies
4
Views
4K
What is the thickness of the wall of a hollow iron sphere submerged in water?
  • · Replies 3 ·
Replies
3
Views
2K
Filling a long tube by submerging it in fluid
  • · Replies 15 ·
Replies
15
Views
3K
How to Determine the Final Velocity of an Iron Block?
  • · Replies 3 ·
Replies
3
Views
1K
Clarification on magnetization and temperature
  • · Replies 12 ·
Replies
12
Views
2K
Finding temperature change, thermodynamics first law
  • · Replies 5 ·
Replies
5
Views
1K
What is the Apparent Weight of an Iron Block Submerged in Water?
  • · Replies 6 ·
Replies
6
Views
6K
Calculate ideal-gas temperature of a material
  • · Replies 2 ·
Replies
2
Views
2K
Change in Entropy When Mixing Water at Different Temperatures
  • · Replies 5 ·
Replies
5
Views
1K
How to calculate initial pressure and temperature - adiabatic process
  • · Replies 7 ·
Replies
7
Views
2K