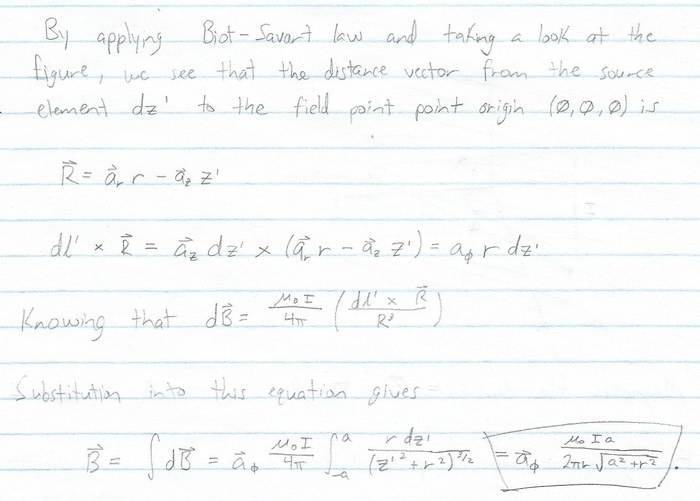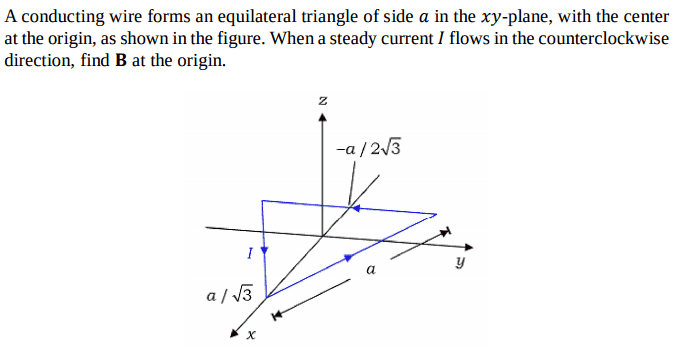
The forum discussion centers on calculating magnetic flux density using the Biot-Savart law, specifically addressing the integration of current elements in the x-y plane. Participants critique the initial approach, highlighting the importance of correctly defining the vectors dl and R, which should only have components in the x and y directions, as the problem is confined to the x-y plane. The necessity of multiplying the final result by three to account for three wires is emphasized, along with the need for clarity on the integration limits from -a to a. The discussion underscores the significance of the right-hand rule in determining the direction of the magnetic field.
PREREQUISITESStudents and professionals in physics and electrical engineering, particularly those focusing on electromagnetism and magnetic field calculations.
You are correct. Neither dl nor R should have components along ez. Since the triangle lies in the x-y plane (z=0), dl should have components along ex and ey. Also, R should only have components along ex and ey because it's pointing from the location of dl , which is in the x-y plane, to the origin, which is also in the x-y plane. Accordingly, the cross product dl x R would come out to be along ez, which is what we should expect from the right hand rule.mfb said: