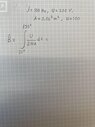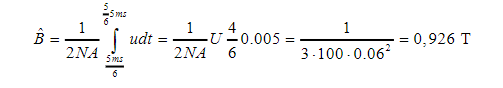Calculating maximum flux density

[JoelKTH]

Homework Statement

Calculating maximum flux density

Relevant Equations

u=dphi/dt=dNBA/dt

Hi everyone,

I have a EE problem that I need to sort out for alternating voltage. I have to find out the maximum flux density.

B_max= integral from 150 degrees to 30 degrees (u/(2NA) dt is my problem.
I have a hard time to integrate this since I am to integrate with time and not degrees or radians. The frequency f= 100 Hz in this problem(not sure if its relevant).
How do I convert degrees to time? To my knowledge the right answer for 150 degrees should be 25/6 ms to 5/6 ms

Necessary data that's not part of my question but in the problem description: U_max= 200 V, A= 0.06^2 m^2, u=dphi/dt=dNBA/dt

Kind regards

 

[Ssnow]

Hi, there is a relation between degrees and time if you have the frequency ... because $f=2\pi \omega$ where $\omega$ is the angular velocity (or pulsation). If you write $\omega=\frac{\Delta \alpha}{\Delta t}$ you have that $\Delta \alpha = \frac{f}{2\pi}\Delta t$, or simply $\alpha=\frac{f}{2\pi}t$ (if it is not a difference), I don't know if this can help you ...
Ssnow

 

[JoelKTH]

Hi, thank you for your reply.

I think some kind of variable substitution is the way to go. If the angular velocity w= d(alpha)/dt ---> dt= w/(d(alpha)) is possible to put into the integral. However using degrees in integral is giving me a maximum flow of about 36.5 T which is way too high.

Is it possible to convert differently?

I attached the integral and the data, perhaps its clearer to understand the problem

 

[Ssnow]

Hi, yes I think the substitution can be of the following form $\alpha \,=\, \frac{50}{\pi}t$ do the differential will be $d\alpha\,=\,\frac{50}{\pi}dt$ and inverting $dt\,=\, \frac{\pi}{50} d\alpha$, now put it into your integral ...
Ssnow

 

[JoelKTH]

Hi,

I tried putting it into the integral. The first try was to convert it to radians and the second to degrees.
I attached my solution and the "right" solution. However I do not get the same answer as below...

Are you sure my attached solution is the way to go?

Kind regards

 

[Ahzmandius]

After 1/100 s you make a full circle -> 360°
Now you can calculate how long you need for 1° respectively 150° etc.
For 150° you''ll get the 25/6 ms
For the 30° it's the same approach.

 

[JoelKTH]

Thank you, I got it :D