Find maximum current in a coil using oscilloscopes and Faraday's Law?

[boysenbeary]

Homework Statement

1. Match each computer graph of Current v. Time to the corresponding oscilloscope graph (think about the functional relation between I(t) and Emf(t). The current, the settings on the oscilloscope, and the oscillation frequencies vary between each run.

2. Derive an equation for Emf(t) by calculating the magnetic field in the region of the detector coil (assume it's size is negligible), then the magnetic flux through the detector coil, then using Faraday's law.

3. For all four runs, use the readout from the oscilloscope pictures and the specifications of the field and detector coils to compute the maximum current in the field coil

Confirm that this number lands close to the value in its corresponding computer graph.

Relevant Equations

field coil:
- radius : R=0.157m
- number of turns in coil : N=100

detector coil
- radius : r=0.013m
- number of turns in coil : n=1000

Current through field coil (oscillates with time)
- I(t) = I_0 * cos(2pi*f*t)

Magnetic Field at Center of a Loop:
- B=(u_{0}*I)/2R

Magnetic Flux:
- I_B = nB(A)

Faraday's Law (number of coils times change in magnetic flux over change in time):
- Emf = -N(d I_B / dt)


Coils (given a oscillating graphs where these measurements are taken at an amplitude peak):
- A : (0.008s, 0.141A)
- B : (0.009s, 0.193A)
- C : (0.002s, 0.089A)
- D : (0.003s, 0.109A)

The experiment consists of a large field coil (connected to a current source) surrounding a coplanar and coaxial small detector coil in the center of the field coil connected to the oscilloscope.

1. Matching Current v. Time Graphs to Oscilloscope Graphs

Example of one pair of graphs (I'll attach others as files)

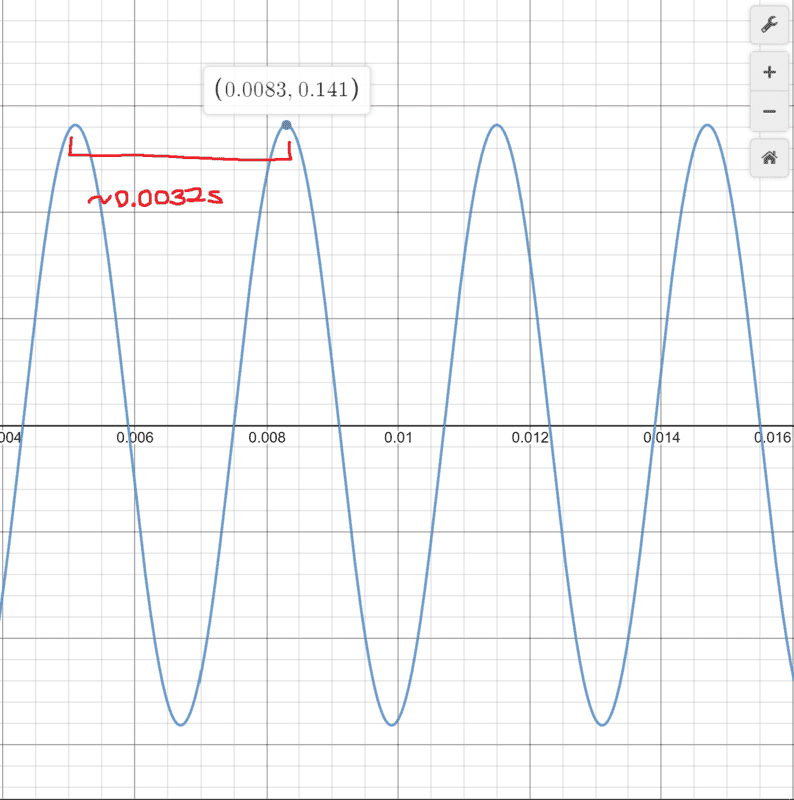
Period ≈ 0.0032s = 3.2ms

( Oscilloscope picture CC BY-NC-SA 3.0 of Libretext and UC Davis Library )

For this section I just want to make sure that I am not making too many assumptions about the functions of I(t) and Emf(t).

Because the I(t) is a cosine graph and (ignoring all the other constants) I derived that you get that Emf(t) is a sin graph with the same (2pi*f*t) within, I assumed that their periods would be the same.

I estimated the period of each current graph and estimated the period of each oscilloscope graph and matched them based on such assumption.

Using this method I matched

A-3, B-2, C-1, D-4

Do you think this is a wrong assumption to make?

2. Derive an equation for emf using Faraday's Law

Started by calculating the magnetic field in terms of I(t) to get

B = [u_o* I(t)]/2R

where R is the radius of the larger field coil

Next I put this into the magnetic flux formula where I had the area of the detector coil to be pi*r^2 and got

I_B = (n*[u_o* I(t)]/2R)(pi*r^2)

where r is the radius of the detector coil and n is the number of turns in the detector oil

Finally, I plugged this into Faraday's Law and did d/dt of I(t) to obtain

Emf = -N * [(n*[u_o]/2R)(pi*r^2)] * I_0 * [-2*pi*f*sin(2*pi*f*t)]

where N is the number of coils in the field loop and f is 1/period3. Calculate the maximum current of the field loop using Faraday's Law, make sure it matches the current graph

So this is where I am stuck. For one of the graphs I have at 0.008s there is a current maximum of 0.141A.

I have an oscilloscope graph which graphs the Voltage Change v. Time

I have a formula (which I have no idea if it's right or not) for Emf that I got using Faraday's Law

I attempted to rearrange the formula to solve for I_0, and got I_0 = (Emf * R) / (pi^2 * N * n * r^2 * f * sin(2pi*t*f)

I'm not sure how I would incorporate the oscilloscope into this equation.

I'm using 1/period to get f which could be wrong.

I'm using 0.008s as t, but I'm not sure if that's the time I need to use.

I'm using the y-values of the oscilloscope for emf, but I don't know if that is what the y-axis measures

It seems like no matter what I plug in, I can't get an answer near 0.141A.

Any help or guidance would be appreciated.

Thank you.

 

[Charles Link]

The experiment is a relatively simple one, but it's unclear what you have for data from the oscilloscopes. I'm expecting to see some kind of sinusoidal voltage reading from the detector coil, but I don't see it. The peak voltage from that should match the computed (sinusoidal) EMF.

 

[boysenbeary]

The experiment is a relatively simple one, but it's unclear what you have for data from the oscilloscopes. I'm expecting to see some kind of sinusoidal voltage reading from the detector coil, but I don't see it. The peak voltage from that should match the computed (sinusoidal) EMF.

Hi Charles, thank you for the response.

When you refer to data from the oscilloscopes do you mean values? I am unfamiliar with oscilloscopes, so from the 4 pictures they provided, all I can take from them is their period and the amplitude of the graph. Is there something else I am missing?

In the formula I derived for I_0, I tried E.m.f values at the peak, but I couldn't get currents anywhere near 0.141A

so I assume that my derivation of the I_0 is incorrect or I am using the wrong values or frequency, time, or e.m.f

 

[Charles Link]

The oscilloscope reading (y-axis) should be so many divisions, scaled by the dial setting of volts per division. You may have included that somewhere, but I didn't see it.
One other thing that I found kind of surprising is the number of turns in the detector coil. Perhaps you have it correct, but $n=1000$ is a lot.
and it might be a typo, but in your formula fot $I_o$ you seem to have omitted $\mu_o$.

 

[Babadag]

1)u_{0}=μo=4*π/10^7 H/m

2)the oscilloscope voltage divisions are 20 mV[see attached]

3) the voltages in oscilloscope are Emf from detector coil.

4)the currents from graph are main coil currents

So, I_0 it is the main coil current.

As I read the periods, I calculate 1/T=f A=300;B=200;C=500;D=400 Hz

The Emf at oscilloscope images are

1-59 mV;2-51 mV;3-56 mV;4-58 mV.

I=Emf/[μo*N/(2R))*n*pi*r^2*2*pi*f]

 

[Charles Link]

This is something the OP should really be doing, instead of the Homework Helpers needing to sift through the data, but I get
A=3 => $V_p=.056$ volts
B=2=> $V_p=.05$ volts
C=1 => $V_p=.056$ volts
D=4 => $V_p=.056$ volts
I agree with the OP's matchings.
If the algebra is done correctly, I think you get
$I_p=(\frac{V_p}{f}) (\frac{R}{Nn \mu_o \pi^2 r^2})$.
I did some arithmetic, plugging in the values, and they were consistent (Edit=I had one arithmetic error that I found=it works now) with
the provided values of
$I_A=.141$ amps
$I_B=.193$
$I_C=.089$
$I_D=.109$
Note: It helps to compute the second factor in $I_p$ above separately=that way you only need to compute it once.