Antoha1
- 14
- 2
- Homework Statement
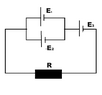
- Three e. sources are connected as shown in the diagram.
What is the current flowing through the conductor and the sources when
it is known that E1=1.3 V, E2=1.5 V, E3=2V, r1=r2=r3=0.2 Ω, (##r##)
R=0.55 Ω.
- Relevant Equations
- Kirchhoff's 1st and 2nd laws;
##V=IR##
I am marking the current flowing through the conductor the same as currect flowing through the E3. (I3)
I am thinking of using Kirchhoff's laws in two contours. 1st contour would be the small one (E1 and E2) counter clock wise. 2nd contour would go through E3,E2,R (wouldn't go through E1).
For 1st contour (CCW):
##E_{1}-E_{2}=r(I_{1}-I_{2})##
2nd contour (CCW):
##E_{3}+E_{2}=I_{3}(r+R)+I_{2}r##
And Kirchhoff's 1st law for left node:
##I_{3}=I_{1}+I_{2}##
Now, that I have system of equations, I can calculate for everyone of them. (only if I applied Kirchhoff's laws correctly, of which I am not sure)
My question is: Did I apply the laws correctly and are these equations OK?
For 1st contour (CCW):
##E_{1}-E_{2}=r(I_{1}-I_{2})##
2nd contour (CCW):
##E_{3}+E_{2}=I_{3}(r+R)+I_{2}r##
And Kirchhoff's 1st law for left node:
##I_{3}=I_{1}+I_{2}##
Now, that I have system of equations, I can calculate for everyone of them. (only if I applied Kirchhoff's laws correctly, of which I am not sure)
My question is: Did I apply the laws correctly and are these equations OK?