SeththeBaller
- 13
- 0
1. The streets of a city are laid out in a rectangular gird, as shown below
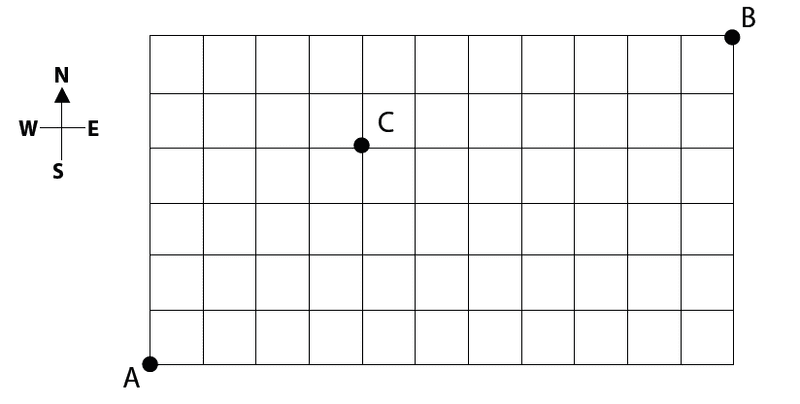
a) Use combinations to find the number of routes through the grid that lead from point A to point B by only traveling north or east. Show your calculations
b) How many of these routes pass through intersections C
2. Alright, so I've solved similar questions before. I get to P(66,6)/6! only to get some absurd answer. I understand that from point A to point B there is a distance of 66 blocks-11 east, 6 north. Somehow I believe that the exponential answer that comes from this is not what my professor expects.
I was wondering if I could have help with this please and thank you :D
a) Use combinations to find the number of routes through the grid that lead from point A to point B by only traveling north or east. Show your calculations
b) How many of these routes pass through intersections C
2. Alright, so I've solved similar questions before. I get to P(66,6)/6! only to get some absurd answer. I understand that from point A to point B there is a distance of 66 blocks-11 east, 6 north. Somehow I believe that the exponential answer that comes from this is not what my professor expects.
I was wondering if I could have help with this please and thank you :D
Last edited: