Calculating the Effects of Lens Closeness on Light Refraction

[hidemi]

Homework Statement

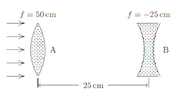
The two lenses shown are illuminated by a beam of parallel light from the left. Lens B is then moved slowly toward lens A. The beam emerging from lens B is:
A. initially parallel and then diverging
B. always diverging
C. initially converging and finally parallel
D. always parallel E. initially converging and finally diverging

The answer is A

Relevant Equations

1/f = 1/f1 + 1/f2 - x/f1*f2

I know what happens initially, calculated as follows.

1/∞ ＋ 1/q = 1/50, q=50

1/-25 + 1/q = 1/-25, q= ∞

However, how do we know about the after when the two lenses get closer to each other?

 

[Steve4Physics]

I know what happens initially, calculated as follows.

1/∞ ＋ 1/q = 1/50, q=50

1/-25 + 1/q = 1/-25, q= ∞

However, how do we know about the after when the two lenses get closer to each other?

Hi. Well no one has answered yet so see if this helps.

Lens A alone forms an image 50cm to its right.

Lens A’s image acts as a virtual object for lens B, initially 25cm to the right of lens B.

As you have done, you can then calculate the initial position of lens B’s image. It is infinity – so the rays from lens B emerge parallel.

If you can figure out how to draw a ray-diagram for lens B with a virtual object, you can do it without any calculations. (Note, lens B’s virtual object is at a focal point of lens B!)

If lens B is now moved left, closer to lens A, then lens B’s virtual object is now further to its right.

If $u, v$ and $f$ are the object-disance, image-distance and focal length of lens B then:

$\frac 1 u + \frac 1 v = \frac 1 f$

$v = \frac {uf}{u – f}$

In this question the numerator of the above equation is always positive because $u$ and $f$ are both negative. The denominator is negative when $u <f$, i.e. when u is more negative than -25cm.

This means when lens B is moved (‘slowly’ or not!) towards lens A, v is always negative.

What does this tell you about the image formed by lens B? And hence what does this tell you about the direction of the rays from B?

Of course, using a ray-diagram for lens B with a virtual object, you could, do this with no calculations!

 

[hidemi]

I got it. Thanks for helping.