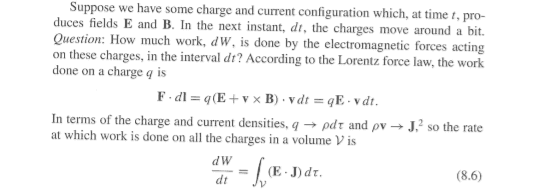I guess I could write it down in tex

##\textbf{F}\cdot d \textbf{l}=q (\textbf{E} +\textbf{v}\times\textbf{B})\cdot \textbf{v}dt=q \textbf{E} \cdot \textbf{v}dt##
current density is defined as ##\textbf{J}=\rho \textbf{v}##
##\textbf{F}\cdot d \textbf{l}=\frac{q}{\rho} \textbf{E} \cdot \textbf{J}dt##
Maxwell-Ampere's law:
##\textbf{E} \cdot \textbf{J}=\frac{1}{\mu _0}\textbf{E} \cdot (\nabla \times \textbf{B})- \epsilon _0 \textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t} ##
the identity
##\nabla \cdot (\textbf{E} \times \textbf{B})= \textbf{B} (\nabla \times \textbf{E}) - \textbf{E} \cdot (\nabla \times \textbf{B})##
We also have
##\textbf{B} \cdot \frac{\partial \textbf{B}}{\partial t}= \frac{1}{2} \frac{\partial }{\partial t} B^2##
##\textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}= \frac{1}{2} \frac{\partial }{\partial t} E^2##
##\textbf{E} \cdot \textbf{J}= \frac{1}{2} \frac{\partial }{\partial t}(\epsilon _0 E^2+\frac{1}{\mu _0} B^2)-\frac{1}{\mu _0} \nabla \cdot (\textbf{E} \times \textbf{B})##
The first term to the right in the last equation is the energy density. We want to look at the energy transported out which is the second term. Since we want what goes out we change the sign
##\textbf{F}\cdot d \textbf{l}=\frac{q}{\rho} \textbf{E} \cdot \textbf{J}dt=\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot (\textbf{E} \times \textbf{B})dt=\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot cB^2dt##
I omitted the direction vector above because I am only looking for a quantification of the energy. Above we still have the units Joule.
Then we look at an EM-wave
##B=\textbf{B}_{0}sin[2\pi ft]=\textbf{B}_{0}sin[2\pi f\frac{x}{c}]##
##\nabla \cdot (B^2)=\textbf{B}_{0} 4 \pi f \frac{1}{c} cos[2\pi f\frac{x}{c}] ##
##\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot cB^2=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f \frac{c}{c} cos[2\pi f\frac{x}{c}]=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f cos[2\pi ft]##
We integrate over a quarter of a cycle since cos is positive in the first quarter and multiply by 4 afterwards
##4\int_{0}^\frac{T}{4}cos[2\pi ft]dt=4\frac{1}{2\pi f}(sin[2\pi f\frac{T}{4}]-sin[2\pi f 0])=2\frac{1}{\pi f}##
##E=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f 2\frac{1}{\pi f}=8 \frac{V}{\mu _0} \textbf{B}_{0} ##
We still have units joule above
If all the energy was sent out from an electrons perspective instead
##\frac{dW}{dt}=\textbf{E} \cdot \textbf{J} d \tau##
By using the rewriting above and again assume that all the energy is sent out and therefore the energy density is 0:
##\frac{dW}{dt}=\frac{1}{\mu _0} \int c \cdot B^2 d \tau##
divergence theorem:
##\frac{dW}{dt}=\frac{c}{\mu _0} \int \nabla B^2 d A=\frac{c}{\mu _0}B^2 4 \pi r^2##
Again we want all the energy to be preserved in one wave
##W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 \int_{0}^T sin^2[2\pi ft] dt##
##sin^2[2\pi ft] =\frac{1}{2}- cos[4\pi ft]##
##W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 \int_{0}^T \frac{1}{2}- cos[4\pi ft] dt##
the lower limit leads to 0 since the integral of cos is sin and we are left with
##W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 ( \frac{T}{2}- sin[4\pi fT])= 2\pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}##
The units are still joule
By equating the two energy relations
##W=8 \frac{V}{\mu _0} \textbf{B}_{0}=2 \pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}##
##4 V= \pi r^2c \textbf{B}_{0}\frac{1}{f}##
##f= \pi r^2c \textbf{B}_{0}\frac{1}{4 V}##
If we assume that we have the ionization energy of hydrogen electron
##E_{ion}=2.1 \cdot 10^{-18}##
We try to detrmine the correpsonding magnetic field of the ionization energy:
##8 \frac{V}{\mu _0} \textbf{B}_{0}=2.1 \cdot 10^{-18}##
But we have two unknowns the volume and the B field. If we instead start with E=hf and see if we can get something that makes sense
##8 \frac{V}{\mu _0} \textbf{B}_{0}=hf##
##8 \frac{V}{h\mu _0} \textbf{B}_{0}=f##
##f4 \frac{V}{c\pi r^2}= \textbf{B}_{0}##
##E=hf=8 \frac{V}{\mu _0} \textbf{B}_{0}=8 \frac{V}{\mu _0} f4 \frac{V}{c\pi r^2}##
It is said that electrons emit photons around the classical electron radius
##r_{classical}=2.82 \times 10^{-15}##
##h=8 \frac{V}{\mu _0} 4 \frac{V}{c\pi r^2}=6.6 \times 10^{-34}##
##V^2=\frac{\mu _0}{32}c\pi r^2 6.6 \times 10^{-34}=\frac{1.26 \times 10^{-6}}{32}3 \times 10^8 \pi (2.82 \times 10^{-15})^2 6.6 \times 10^{-34}##
##V^2=19.5 \times 10^{-62}##
##V=4.419.5 \times 10^{-31}##
This volume seems to be close to the 1s volume.
In general
##h=2.7 \times 10^{-2} \frac{V^2}{r^2}=6.6 \times 10^{-34}##
The second energy relation obtained above:
##2 \pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}=E##
## r^2B_{0}^2 =\frac{f\mu _0}{c2 \pi}E=\frac{E}{2.7 \times 10^{-2} \frac{V^2}{r^2}}\frac{\mu _0}{c2 \pi}E##
## V^2B_{0}^2 =\frac{E}{2.7 \times 10^{-2} }\frac{\mu _0}{c2 \pi}E=0.0255 \times 10^{-12}E^2##
## VB_{0} =1.59 \times 10^{-5}E##
and the first energy relation obtained above:
##8 \frac{V}{\mu _0} \textbf{B}_{0}=E##
##V \textbf{B}_{0} =\frac{\mu _0}{8}E=1.58 \times 10^{-5}E##