LCSphysicist
- 644
- 162
- Homework Statement
- .
- Relevant Equations
- (1 + a^x)^(a^(-x))
(1 + a^x)^(a^(-x))
Let's assume a, say, two.
the limit of it, with x tending to infinity,
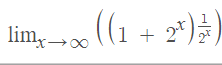 is one, but i was thinking...
is one, but i was thinking...
Calling 2^x by a, we have that when x tend to infinity, so do a, So:
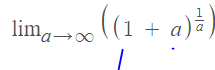 that is euler number no? Contradictory... where am i wrong?
that is euler number no? Contradictory... where am i wrong?
Let's assume a, say, two.
the limit of it, with x tending to infinity,
Calling 2^x by a, we have that when x tend to infinity, so do a, So: