Calculating the Perimeter and Area of a Square MIKE

[spiritzavior]

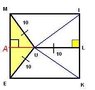
1. given a square MIKE, point U, U is an interior point, L is the midpoint of IK, then MU is a segment equal to segments EU and LU which is equal to 10 units. What is the perimeter of MIKE and the Area of IULK?
2. P= 4s, A=1/2h(b1+b2)
3. P=4(20), P=80
A=1/2(10)(10+20), A=5(30),A=150
I don't know what theorem/s to apply.
Is it correct? if not please help?thanks

 

[ehild]

Could you please show a picture of the problem?

ehild

 

[spiritzavior]

I don't know how to post the picture here.

 

[ehild]

Draw a picture, save it. Writing your post, click on Go Advanced. Under the title Additional Options below, choose Manage Attachments. Choose browse and upload.
I do not know in what sequence do M,I,K,E are assigned to the vertexes of the square. Is the attached drawing correct?

ehild

 

[spiritzavior]

Could you please show a picture of the problem?

ehild

a little changes needed abd there are 3 segments undrawn.

here it is.

 

[ehild]

Congratulation, you could upload a picture!

My problem is that the line IULK is not closed, how can it enclose an area?

Anyway, you can determine the side-length of the square. What kind of triangle is the yellow one? What is the ratio between the lengths of UI and UK? Draw the line LU further till it crosses the side of the square at A: What angles are at A and L?

ehild

 

[spiritzavior]

thanks for guiding me here.

the yellow triangle is an isosceles.
UI and UK have the same length.
Line AL is perpendicula to Lines MF and IK, creating right angles.

and I'm looking for the area of FULK.

how do I solve this? what treorem/s should I use?

 

[ehild]

Correct.

The area of FULK? Where is F?

You need the side of the square first. The segment AL has the same length as the sides of the square. (It is parallel with MI and EK, and bounded by the parallel lines ME and IK.) If x is the length of one side of the square AU = x-10. Then use Pythagorean theorem to find x.

ehild