Jerry1989
- 4
- 0
Hey Guys,
I'm stuck with this problem, we want to compare the curve of a beam to it's horziontal deflection, it's for an experiment we're performing on a very elastic beam.
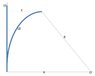
In the attachment you see a flexibel beam getting deflected by a force, this causes displacement x. We don't know (or can't measure) displacement in vertical y-direction.
However, we can assume the beam bends in a way that it's curvature resembles a circle with radius R.
Now, if we have an L0 of 120mm and an X-displacement of 55mm. What would that radius R be?
So far, I've tried an arc-length menthod, and I tried looking at the circles, but I just can't figure it out. Can you guys help me out?
I'm stuck with this problem, we want to compare the curve of a beam to it's horziontal deflection, it's for an experiment we're performing on a very elastic beam.
In the attachment you see a flexibel beam getting deflected by a force, this causes displacement x. We don't know (or can't measure) displacement in vertical y-direction.
However, we can assume the beam bends in a way that it's curvature resembles a circle with radius R.
Now, if we have an L0 of 120mm and an X-displacement of 55mm. What would that radius R be?
So far, I've tried an arc-length menthod, and I tried looking at the circles, but I just can't figure it out. Can you guys help me out?