Discussion Overview
The discussion revolves around the calculation of the surface area of a sphere using differential area elements (dA). Participants explore the mathematical expressions involved, particularly the roles of angles and the integration limits, as well as the geometric interpretations of these elements.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
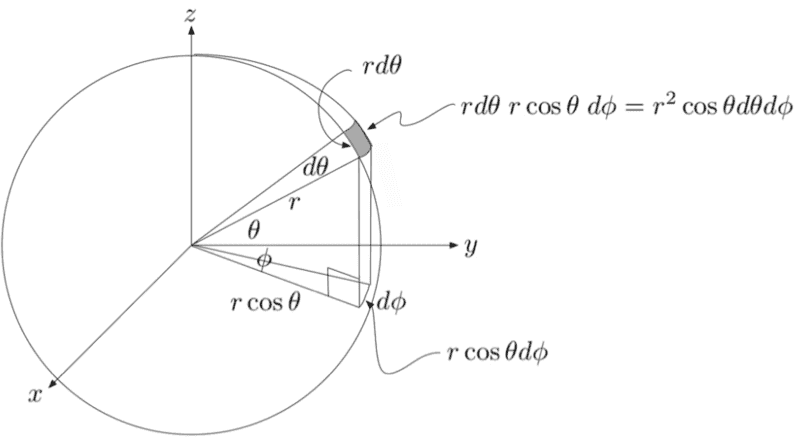
- Some participants express confusion regarding the use of ##rcos\theta d\phi## versus ##rd\phi## for calculating surface area, questioning the necessity of the cosine factor.
- There is a discussion about the integration limits for ##\theta##, with some suggesting it should range from ##-\frac{\pi}{2}## to ##\frac{\pi}{2}## based on the definition of the angle from the south to north pole.
- Participants propose that the surface area of a ring at a fixed ##\theta## should be calculated using the correct circumference, which involves the cosine factor due to the curvature of the sphere.
- Some participants challenge the geometric interpretations of circles drawn in relation to the sphere, debating whether certain circles fit the curvature appropriately.
- There are references to polar coordinates and transformations that relate different angle definitions, indicating a complexity in the coordinate system used.
- One participant emphasizes that the standard approach to calculating the surface area involves parallel slices to the xy-plane, which contrasts with the tilted red circle proposed by another participant.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct approach to defining the differential area element or the geometric interpretations of the circles involved. Multiple competing views remain regarding the necessity of the cosine factor and the appropriate integration limits.
Contextual Notes
There are unresolved questions about the assumptions underlying the geometric representations and the definitions of the angles used in the calculations. The discussion highlights the complexity of integrating over a sphere and the implications of different coordinate systems.