Calculating the Volume Between Three Surfaces: Is My Approach Correct?

[nejla]

Dear all,

I do really need your help.
I'd like to find the volume contained between a sphere (x^2+y^2+z^2=r^2) , plane1 (ax+by+cz+d=0), and plane2 (z-h=0).

Would you please check what I've done till now?

From the sphere and plane1 equations I got:
x1=sqrt*(r^2-y^2-z^2)
x2=d/a-(b/a)y-(c/a)z

Then, by assuming that x1=x2 (as the sphere and plane1 intersect), I derived two equations: one for y1 and one for y2 as follow:
y1=f(z)
y2=g(z)

Also, by assuming y1=y2, I got:
z1=M (a constant value)
z2=N (a constant value)

Now, let assume z1<h<z2

So, to derive the volume I thought that I can run three integrals as bellow:

A=int(1,x,x1..x2)
B=int(A,y,y1..y2)
volume = int(B,z,h..z2)

Am I right? Would you please let me know that what I am doing is right or not?

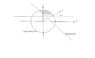
I also drew a simple picture. The shaded area represents the portion of the sphere that I am looking for its volume.

Thanks in advance,
Nejla

 

[nejla]

Hi again,

I tried it for a special case where plane1 is x=0 and I got the right answer. But for the general case where plane1 is ax+by+cz+d=0, I cannot calculate the integrals.

For the general case I have:

x1=- d/a - (b*y)/a - (c*z)/a

x2=(r^2 - x^2 - y^2)^(1/2)

y1=-(a*(a^2*r^2 - a^2*z^2 + b^2*r^2 - b^2*z^2 - c^2*z^2 - 2*c*d*z - d^2)^(1/2) + b*d + b*c*z)/(a^2 + b^2)

y2=-(b*d - a*(a^2*r^2 - a^2*z^2 + b^2*r^2 - b^2*z^2 - c^2*z^2 - 2*c*d*z - d^2)^(1/2) + b*c*z)/(a^2 + b^2)

z1=-(c*d + (a^4*r^2 + 2*a^2*b^2*r^2 + a^2*c^2*r^2 - a^2*d^2 + b^4*r^2 + b^2*c^2*r^2 - b^2*d^2)^(1/2))/(a^2 + b^2 + c^2)

z2=-(c*d - (a^4*r^2 + 2*a^2*b^2*r^2 + a^2*c^2*r^2 - a^2*d^2 + b^4*r^2 + b^2*c^2*r^2 - b^2*d^2)^(1/2))/(a^2 + b^2 + c^2)

I do really need your help.
Thanks in advance,
Nejla

 

[nejla]

Thank you all. I eventually solved my problem. Whenever I get the chance, I will write down its answers here.Nejla