Calculating Thickness of Lenses for Max. Reflection: n1, n2, λ

[toothpaste666]

Homework Statement

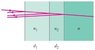
A highly reflective mirror can be made for a particular wavelength at normal incidence by using two thin layers of transparent materials of indices of refraction n1 and n2 (1 < n1<n2 ) on the surface of the glass ( n>n2 ).(Figure 1)

A)What should be the minimum thicknesses d1 in the figure in terms of the incident wavelength λ, to maximize reflection?Express your answer in terms of the variables n1, n2, and λ.

B)
What should be the minimum thickness d2 in the figure in terms of the incident wavelength λ, to maximize reflection?
Express your answer in terms of the variables n1, n2, and λ.

Homework Equations

2t = (lamda n)
(lamda n) = lamda/n

The Attempt at a Solution

they want us to maximize reflection so that means they want constructive interference so we use

2d_1 = (lambda_n) = lamda/n_1

d_1= lambda / 2n_1

i put this as my answer for part a but it was wrong. I am guessing I need to include n_2
in my equation but i am not quite sure how to relate them. can someone point me in the right direction?

 

[toothpaste666]

I think the main reason i am confused is that i don't see how the index of refraction n2 would affect the thickness d1. it seems that n1 and n2 would affect d2 but only n1 would affect d1

 

[toothpaste666]

oh wait i accidently entered it into mastering physics as n1(lambda/2) -__- i turned out to be right about that one

 

[toothpaste666]

so for the part B)
the wavelength of the light entering d2 is lambda/n1
2d_2 = \frac{\frac{lambda}{n_1}}{n_2}

d_2 = \frac{lambda}{2n_1n_2}

is this correct?

 

[toothpaste666]

or would it undergo a 180 degree phase shift and be
d2 = lambda/4n1n2