Calculating total bulk modulus of cylinder, piston and oil

[Paavo Palikka]

Hello,

I have been thinking about following problem: I have some kind of piston and cylinder with oil. I know the pressure in oil. Let's say it is 500bar. I would want to know how much is displacement of piston.
Let's say bulk modulus of oil is 3Gpa.
Let's also say that bulk modulus of materials in piston and cylinder is 50Gpa.

How should I get the total bulk modulus of the system? It somehow seems that I can't just calculate it followingly:

...

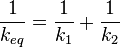Should I somehow take volumes into account? What is right equation?



-Paavo Palikka

 

[Baluncore]

I have some kind of piston and cylinder with oil. I know the pressure in oil. Let's say it is 500bar. I would want to know how much is displacement of piston.

If the piston is externally constrained by a rod, but free to move in the cylinder, then it becomes a constraint or fluid volume problem. You need to better specify the constraints.

Most energy in hydraulic systems is stored in the hoses, pipe and fluid volume.
500 bar is 2 or 3 times the pressure typically used in the hydraulics industry.

 

[PeterF]

Further to Bulancore's reply the bulk modulus of oil is about 1.5 GPa the bulk modulus of steel is about 160. In most cases the oil volume is by far the dominant term in your equation above so for practical purposes you can effectively ignore the rest of the components. If you need high accuracy you have to account for the expansion of the oil hoses, the volume of oil in the hoses as well as the cylinder then the stretch and expansion of the cylinder before compression of the piston would become an issue.

 

[Paavo Palikka]

Thanks for your answers!

I forgot to tell that this is rather theoretical question. 500 bar pressure piston creates as well as bulk modulus of fluid and, piston and cylinder can be anything. They are not important, I am just curious about the way effective (total) bulk modulus would be calculated.

Baluncore: I am not sure what external constrains to piston means. Piston creates 500bar (or any other) pressure to fluid and therefore it is at least easy to think it is constrained from outside with 500bar pressure.

Therefore I am curious what is the equation(s) that should be taken into account when calculating effective bulk modulus. Does it have something to do with volumes of parts of this system? Or geometry?..

 

[Chestermiller]

The concept of bulk modulus is based on the constraint that the loading is applied isotropically to the material. In this system, while the loading is isotropic on the fluid, it is not isotropic on either the cylinder or the piston. So trying to apply the term bulk modulus to a system with this kind of loading is meaningless.

Chet

 

[Paavo Palikka]

Cherestermiller: Thanks for your answer! However I have to disagree, one of the first hits by googling effective bulk modulus is http://www.atp.ruhr-uni-bochum.de/rt1/currentcourse/node89.html. It is quite easy to find other articles like this also by googling. However I have problems understanding how calculation of effective bulk modulus for my system goes.

 

[Chestermiller]

Cherestermiller: Thanks for your answer! However I have to disagree, one of the first hits by googling effective bulk modulus is http://www.atp.ruhr-uni-bochum.de/rt1/currentcourse/node89.html. It is quite easy to find other articles like this also by googling. However I have problems understanding how calculation of effective bulk modulus for my system goes.

I guess I must be missing something. What is your precise definition of the quantity you call Effective (or Equivalent) Bulk Modulus? Please describe how it would be measured experimentally.

I can see how an equivalent/effective bulk modulus can be defined for a composite material that is loaded isotropically from the outside, but I have no idea what they are referring to in the link you sent when they talk about the bulk modulus of a thick walled cylindrical container since, somehow, the implication is that the container is being loaded neither uniformly nor isotropically.

Chet

 

[Baluncore]

You want displacement of the piston, but you have not specified the reference for displacement measurement. You have not identified if the oil pressure is provided by pumping fluid or loading the ends of the hydraulic cylinder. You have not identified the fluid pressure situation on the rod side of the piston. You have not specified external hydraulic connections.

If a cylinder containing oil is sealed then compression of the system will have several effects. The fluid density will increase slightly due to compression. The cylinder diameter will increase due to fluid pressure. The piston, piston rod and cylinder end will shorten due to axial compression.

Minor effects will be: The length of the outer cylinder will not change due to pressure since the piston is a sliding oil seal, however, the part of the cylinder containing oil under pressure will expand in diameter, which may result in a shortening of the cylinder material and so a relative change in the piston face to cylinder surface position. The piston ring groove depths, the pressure faces involved and the rod penetration may make computation of a bulk modulus for the piston quite complex.

If we model your system as a simple hydraulic jack, the "total" bulk modulus becomes the series connection of the bulk moduli of the cylinder end, the fluid, the piston, the rod and the rod end.

 

[Baluncore]

The reciprocal of the sum of reciprocals is only applicable for layers of equal thickness and bearing area.

Consider a long fluid column with a short rod. Then consider a short fluid column with a long rod. It is clear that the “total” bulk modulus for a system must be computed from the weighted bulk moduli of all the components.

For real systems, each term must be weighted by the length and sectional area of each component.

 

[Paavo Palikka]

Chestermiller: Well at least in my mind effective bulk modulus refers to kind of stiffness of object. As seen in bulk modulus equation:

This answers question "how much volume changes when certain pressure is applied". I think whole object does not need to be pressurized. As an example in my question cylinder rod is pressurized only from one end. Of course then effective bulk modulus is different than when whole object would be pressurized but this still answers the question "how much volume changes when certain pressure is applied". Hopefully I am clear with my text here

 

[Chestermiller]

Chestermiller: Well at least in my mind effective bulk modulus refers to kind of stiffness of object. As seen in bulk modulus equation:

This answers question "how much volume changes when certain pressure is applied". I think whole object does not need to be pressurized. As an example in my question cylinder rod is pressurized only from one end. Of course then effective bulk modulus is different than when whole object would be pressurized but this still answers the question "how much volume changes when certain pressure is applied". Hopefully I am clear with my text here

You can dream up whatever definition you want. But the standard definition of bulk modulus in thermodynamics and mechanics is that the compressive stress on the body is uniform and isotropic. If you want to use your own definition, then you're on your own.

Chet