Calculating Tray and Food Weight: Torque Question Help Requested

[Student3.41]

Homework Statement

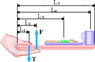
A lunch tray is being held in one hand, as the drawing below illustrates.
The mass of the tray itself is 0.218 kg, and its center of gravity is located at its geometrical center. On the tray is a 1.28-kg plate of food and a 0.255-kg cup of coffee. Assume L1 = 0.0590 m, L2 = 0.109 m, L3 = 0.242 m, L4 = 0.373 m and L5 = 0.398 m. Obtain the force T exerted by the thumb (enter first) and the force F exerted by the four fingers. Both forces act perpendicular to the tray, which is being held parallel to the ground.

Attached picture.

Homework Equations

T=Fl

The Attempt at a Solution

I first solved for F.

I have subtracted L₁ all the other L values because I have started from the thumb.

T_cup = Fl = (0.255kg*9.8m/s^2)(0.373m-0.0590m) = 0.785N*m

T_food = (1.28kg)(9.8m/s^2)(0.183m) = 2.30N*m

I am not sure about this one but I am thinking I use the CG as the L because it is uniform. Therefore;

T_tray = (0.218kg)(9.8m/s^2)(0.200m(CG)-0.0590m) = 0.301N*m

T_F = Fl = F(0.05m)

T[/SUB]NET[/SUB] = 0 - - - > Static Equilibrium


T_F = T_tray+T_food+T_cup
F(0.05m) = 0.301+2.30+0.785

F(0.05m)= 3.39N*m
F=3.39/0.05
F=67.8N


F[/SUB]NET[/SUB] = 0 ------> Equilibrium, Calulate the Weights of the objects.

W[/SUB]tray[/SUB]W[/SUB]cup[/SUB]W[/SUB]food[/SUB]F[/SUB]f[/SUB]
(2.14N) + (12.5N) + (2.50N) + (-67.8N) = T
T=-51.0N (-) indicates direction.

Did some work and need help.. thanks.

 

[PhanthomJay]

Your work approach looks very good. To be sure you did not make a math error, it is always a good idea to sum moments about the other unknown force (about the fingers) to see if you get the same result for T. Good work.