Calculation for Charge/Discharge Current

[HelloCthulhu]

Hello again members!

I'm trying to boost a 6v lantern battery to 12v to power a 14w light bulb. I'm using these elements as a template for learning more about how IC regulators and boost conversion work. I've added an image of the prefabricated boost converter I bought online as an attachment.

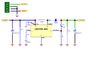
I've been gettting conflicting information regarding parallel rc circuit equations with a DC source. I feel like I'm getting nowhere , so I'm seeking help from the experts. Using a 6v lantern battery as the voltage source, how do I calculate the charging/discharging current at node 1 (1kuF/63v capacitor) and the current at node 2 (10kOhm resistor)?

I greatly appreciate your assistance! :shy:

 

[NascentOxygen]

Hi HelloCthulhu! Does it not work? Or why are you needing to do these calculations? What instructions are you given to change or select the capacitors?

If you own a DC voltmeter, can you connect it in parallel with the input capacitor and note how much that reading changes when you connect/disconnect the 15W globe at the output?

Operating a 14W device off a 6V lantern battery will give the battery a short life, you no doubt appreciate that.

 

[HelloCthulhu]

Hi NascentOxygen

Thank you for the quick response! The boost converter I purchased works fine. I'm really just using it as an example to learn more about IC regulators and boost conversion. I found an equation for calculating the first parallel RC circuit, but it’s for an AC source. Is it the same for a DC source?

 

[NascentOxygen]

The input capacitor definitely needs to be large enough, especially when powering from a dry cell battery with its higher resistance. But the R's are not important that I can see. So long as the voltage across the input C doesn't drop much when you connect the maximum load, then that C is large enough. The calculation is probably not straightforward, I haven't looked into it.

 

[HelloCthulhu]

Thanks again for the response.
This is the equation I found for capacitor charging current:
ic = (Vs/R) e-t/RC
This is the equation I found for capacitor discharging current:
I = Io e-t/CR
What I can’t figure out is how to calculate the inductor current when the switch is closed. Are you familiar with RCL circuits?

I greatly appreciate any information you can provide me with.

 

[NascentOxygen]

Thanks again for the response.
This is the equation I found for capacitor charging current:
ic = (Vs/R) e-t/RC
This is the equation I found for capacitor discharging current:
I = Io e-t/CR

Those are just general equations, and won't help you much here.

What I can’t figure out is how to calculate the inductor current when the switch is closed. Are you familiar with RCL circuits?

The inductor current will vary with time, and according to the load. But its average value will be (almost) exactly equal to the average value of your load current.

I think you should do a web search for a description of how one of these works, where they will highlight its operation with graphs of relevant current and voltage waveforms around the circuit.

 

[HelloCthulhu]

Those are just general equations, and won't help you much here.

Which equations should I use to apply KCL/KVL and/or Ohm's Law to this circuit?

I think you should do a web search for a description of how one of these works, where they will highlight its operation with graphs of relevant current and voltage waveforms around the circuit.

I found the current equation for RLC circuits, but what I'm really looking for is how to calculate voltage and current at each node of a complex circuit. In the example the elements are parallel or in series. Node 1 and node 2 are parallel. But node 3 (100uH inductor) is in series with node 2 and node 4 (100nF capacitor) shares a connection with node 2 to Pin 5 of the LM2577. Node 5 is connected to Pin 4. Learning the node analysis for this circuit will help me understand complex circuits as well as how to use ICs for boost conversion. Could you show me how to calculate the total current for the first 5 nodes of this circuit when the NPN switch is closed?

I greatly appreciate all of your assistance!

 

[NascentOxygen]

The most interesting waveform is of current in the inductor. When the switch connects pin 4 to ground you have the inductor with a steady 6V on one end and 0V on the other. The equation for the voltage across a low resistance inductor is: v(t) = L· di/dt[/size].

With v(t) held approximately constant by the large capacitor and L=100μH this gives us
di/dt = 60000 amps/sec, meaning the current in the inductor increases linearly at the rate of 60000 amps per second. Hopefully the circuit is designed so that well before the current reaches a huge level and drains the capacitor something inside the IC will open that switch and disconnect pin 4 from ground. When this happens the current in the inductor will cease increasing, but while it continues to flow the diode directs the current into the output capacitor. That capacitor is chosen to be of large value so that this burst of current into it is absorbed with barely a change in that capacitor's voltage. Consequently, the output voltage is going to be fairly smooth DC.

I hope that helps.

 

[vk6kro]

Your diagram shows the chip to be a LM2755 but you mention a LM2577 which seems more likely.

The heart of this chip is a square wave oscillator whose duty cycle can be changed by the voltage on the feedback pin.

This oscillator switches a transistor on and off and this causes pulses of current to flow in an inductor.
This produces large voltage pulses to be generated and these are passed through the diode to charge up the large capacitor at the output.

This charging continues and a fraction of the output voltage is passed by a voltage divider (100K / 2K) to the feedback pin.

When this fraction reaches a certain voltage (about 1.3 volts), the output pulses become very narrow, so charging almost stops. The output voltage then remains steady.

If a load tends to reduce this voltage, then the feedback voltage drops and wider pulses are fed to the switching circuit and more charging happens to bring the voltage back up to the required level.

The output voltage across the capacitor never really gets to fully discharge into a load because the circuit keeps recharging the capacitor.

 

[NascentOxygen]

@vk6kro. HelloCthulhu will appreciate your description of how his module works. All looks correct except:

This oscillator switches a transistor on and off and this causes pulses of current to flow in an inductor. This produces large voltage pulses to be generated

There are no "large voltage pulses" anywhere here. For a step up to from 6V to 12V as the OP will be using, peak voltage across his inductor will never exceed ~7V.

 

[vk6kro]

@vk6kro. HelloCthulhu will appreciate your description of how his module works. All looks correct except:

There are no "large voltage pulses" anywhere here. For a step up to from 6V to 12V as the OP will be using, peak voltage across his inductor will never exceed ~7V.

There are certainly large voltage spikes available in this circuit. The voltage divider has a possible ratio of 51 to 1 so the potential output voltage is 1.3 volts times 51 or about 66 volts.

Setting the 100 K pot to give 12 volts out is optional. That was a description of how the chip operated, not how this application would use it.

 

[NascentOxygen]

Just so OP knows he shouldn't expect to be seeing any large voltage pulses in his circuit. Or if he does, something is amiss.

 

[vk6kro]

Just so OP knows he shouldn't expect to be seeing any large voltage pulses in his circuit. Or if he does, something is amiss.

Assuming the position of the 100 K pot is random when the power is first applied, a large voltage may be produced until the circuit is adjusted.

 

[HelloCthulhu]

Thank you both for all of your help! I'm really beginning to understand how this circuit operates. However, I still need help finding the total current of the circuit when the switch is closed. I hope you both could answer a few more questions for me:

The equation for the voltage across a low resistance inductor is: v(t) = L· di/dt.

I understand how this equation works. But since this is an RLC circuit, how is the current at node 3 (100uH inductor) influenced by node 1 (1kuF/64 volts capacitor) and node 2 (10kOhm resistor)?

This is the equation I found for capacitor charging current:
ic = (Vs/R) e-t/RC
This is the equation I found for capacitor discharging current:
I = Io e-t/CR
Can I use these equations to calculate current for the parallel RC circuit at node 1 (1kuF/64 volts capacitor) and node 2 (10kOhm resistor)? If not, which equation should I use?

I really appreciate all of the information you both have provided me. Thanks again!

 

[vk6kro]

When you first switch on, the main effect will be caused by the large capacitor at the left of the diagram.
The current in this will depend on the 6 volt supply and how much internal resistance it has, but it is likely to be very high.

But I wonder if you read the description of how this circuit works? Did you understand it?

Can you see that the behaviour of this circuit is mostly controlled by the integrated circuit and not so much by the external components?
This is not a pure DC circuit and it works on pulses which vary in width and amplitude.

You seem to be calling components "nodes". Nodes are the joining points of components, not the components themselves.