annamal
- 393
- 33
I am confused at this calculation of the electric flux through a trapezoidal surface. The flux in should equal the flux out.
The flux in equals -E*A1 where A1 is the area of the bottom of the trapezoid. The flux out equals E*A2 where A2 is the area of the top of the trapezoid. But the two fluxes aren't equal due to differing areas. We are only considering the bottoms of the trapezoid since the electric field only flows there as shown in the image.
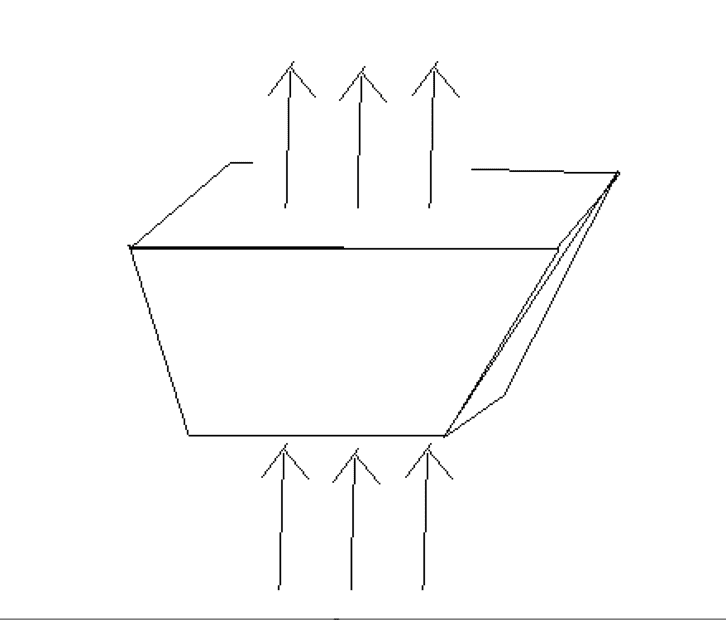
The flux in equals -E*A1 where A1 is the area of the bottom of the trapezoid. The flux out equals E*A2 where A2 is the area of the top of the trapezoid. But the two fluxes aren't equal due to differing areas. We are only considering the bottoms of the trapezoid since the electric field only flows there as shown in the image.