Calculations for a capacitor charging from another capacitor

[cjs94]

Hi all,

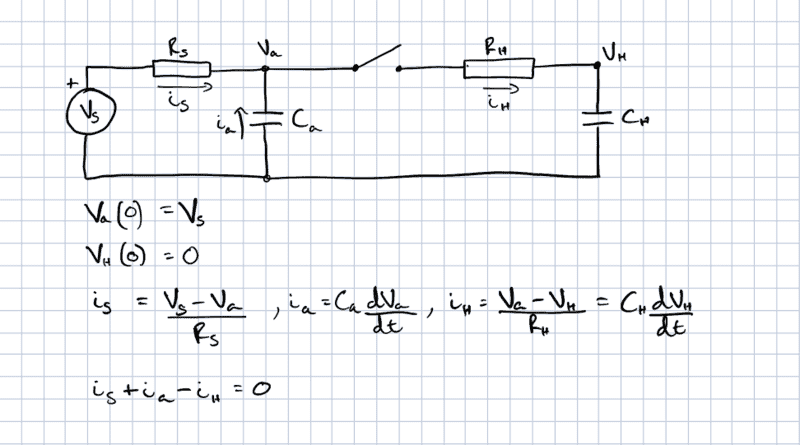
I'd appreciate help in calculating the voltages in the circuit shown. I thought it should be fairly straight forward, but it has me stumped. This is a sample-and-hold circuit for an ADC -- the switch is closed to charge the hold capacitor with the sample voltage and then opened to isolate during conversion. I'm trying to model the charging profile of the hold capacitor when the switch is closed.

I've shown the initial conditions as well as the basic circuit equations, but I can't figure out how to actually solve it, mainly I think because the differentials are sort of co-dependent.

Thanks in advance,
Chris

 

[gneill]

Are actual component values given, or perhaps some relationships between them? For example, if the time constant of the left hand side RC pair is much greater than that of the right hand side pair, you can make certain simplifying approximations...

 

[cjs94]

Are actual component values given, or perhaps some relationships between them? For example, if the time constant of the left hand side RC pair is much greater than that of the right hand side pair, you can make certain simplifying approximations...

Sure. The right-hand side is the input stage of a PIC18, so C_H = 10pF and R_H is about 8.5k (for Vcc = 3.3V). The left-hand side, Vs = 2.11V and R_S = 825k -- the actual circuit is a 4.7M/1M divider from 12V, I just simplified it to a Thevenin equivalent. C_a = 100nF. So, l.h.s. RC >> r.h.s. RC.

My reason for the calculation is that the maximum recommended source impedance is 10k. Without C_a the source impedance is obviously much greater than that, however I realize that I have no idea how to think about the effect of C_a on that impedance in response to an impulse event (which is effectively what happens when the switch is closed). My intuition (right or wrong) tells me that C_H will see a very low impedance by virtue of C_a, until the charge on both capacitors has equalised, then the impedance should rise substantially as both capacitors continue to charge from V_s. I'm looking for a formal way to characterise that.

While I have actual values, I would like to know how to approach this from first principles, since it is something that I thought I understood and should be able to do. I was wrong.

Regards,
Chris

 

[gneill]

Okay, looks like you've got a handle on how the circuit will behave overall.

As to a formal approach, my suggestion would be to employ Laplace Transforms and solve the circuit in the s-domain via the usual KVL and KCL methods (nodal or mesh analysis).

You should be able to confirm your results using a simulator such as LTSpice.

 

[gleem]

One of the complications of this circuit when is it requires you to set up and solve a second order differentiation equation.

 

[Babadag]

At first I think is-ia-ih=0 [if Va potential is more than Ca potential].
Second dVa(t)/dt>>s*Va(s)-Va(0)[=Vs] and dVh/dt>>s*Vh(s) [Vh(0)=0].
From is-ia-ih=0 and is*Rs+ih*Rh+∫ih.dt/Ch=Vs you'll get something like:
Vh(s)=(As^2+B*s+C)/(D*s^3+E*s^2+F*s+G)
It's a lot to calculate that's all.

 

[gleem]

At first I think is-ia-ih=0 [if Va potential is more than Ca potential].

V_a is always equal to V_c

Second dVa(t)/dt>>s*Va(s)-Va(0)[=Vs] and dVh/dt>>s*Vh(s) [Vh(0)=0].

Your notation makes no sense to me, what is s? are you doing something with Laplace transforms?

 

[Babadag]

If Va=Vc no current will flow to Ca. The symbol “>>” it means " the Laplace transform is"

 

[Babadag]

You can start from the idea Vh = 0 for t = 0 and Vh = Vs for t = [infinite] and it is constantly increasing. Then Vh=Vs[1-e^(-t/k)]. ih=dVh/dt/Ch and ih*Rh+Vh=Va

 

[vela]

While I have actual values, I would like to know how to approach this from first principles, since it is something that I thought I understood and should be able to do. I was wrong.

You can combine the equations you have to get
\begin{align*}
\frac{dV_\text{H}}{dt} &= \frac{1}{R_\text{H}C_\text{H}}(V_\text{a}-V_\text{H}) \\
\frac{dV_\text{a}}{dt} &= \left(\frac {1}{R_\text{H}C_\text{a}}+\frac{1}{R_\text{s}C_\text{a}}\right)V_\text{a} - \frac{1}{R_\text{H}C_\text{a}}V_\text{H} - \frac{1}{R_\text{s}C_\text{a}}V_\text{s}
\end{align*} (or something similar if I made algebra or sign mistakes). You can solve this system using matrix methods.

If you're not familiar with that method, you could solve the first equation for $V_\text{a}$ and then plug the result into the second equation to get a second-order differential equation for $V_\text{H}$.

 

[Babadag]

Matrix method it is a very interesting idea. See-for informations:
http://personal.stevens.edu/~llevine/ma227/systems_des.pdf

 

[cjs94]

Thanks for all the replies. I have some reading to do!