Van Allen
- 1
- 0
i need to finish this before i move on tomorrow. any help? thanks
Points M and N are the midpoints of opposite sides of paralellogram ABCD. Prove that:
a) R and S trisect diagonal BD
b) R is a points of trisection of AN and S is a point of trisection of MC.
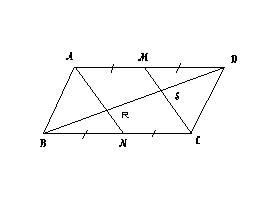
Points M and N are the midpoints of opposite sides of paralellogram ABCD. Prove that:
a) R and S trisect diagonal BD
b) R is a points of trisection of AN and S is a point of trisection of MC.