Can Resolving Forces Differently Lead to Contradictory Equations?

[HvB99]

Hi ! So a friend and I were solving some mechanics problems in class today. And we came across a pretty funny mathematical paradox. So basically we tackled the problem in different ways...but we ended up with different equations...and none of us could prove the other wrong !
So here goes...
The Problem:

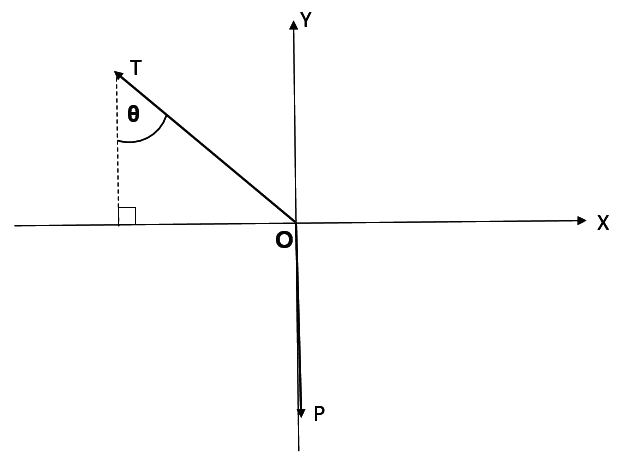
The question...a very simple one really :
"Express T in terms of P"
1) His method...(or as he describes it "The Human Method")

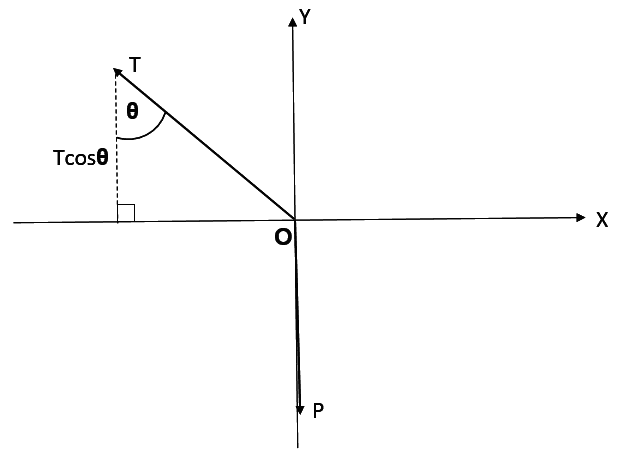
He resolved vertical component of the force T, ie. Tcosθ
Then he equated vertical components saying P = Tcosθ... therefore T = Psecθ

2)My way...
Note: This was part of a much complex problem... I'm not possessed to go through sooooo much trouble for such a small thing...and well...if i hadn't i wouldn't have found this...anyway

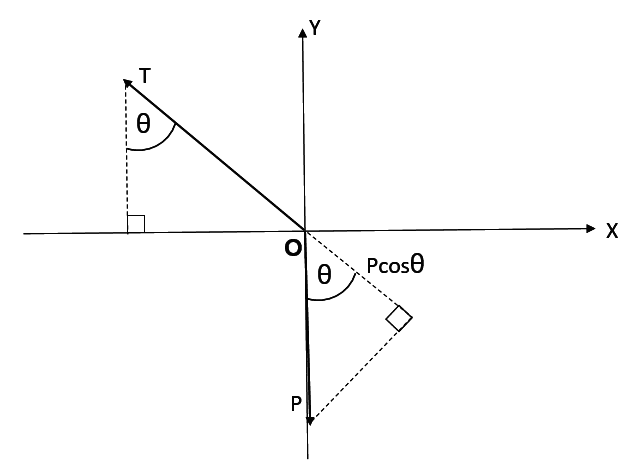
I resolved P instead,
and got that T = Pcosθ...the exact opposite

SO...the big question is ...
T = Pcosθ vs. T = Psecθ

Now ... i know practically speaking I might be wrong ...because according to me T < P ...however T would have to be greater ...since its offsetting the downward vertical force of P and has a leftward horizontal component...but then again ...can't you make the same argument about resolving P ??

I know .. I've been blabbering alot...but it really seems mind boggling !
Mathematically both seem correct XDUpdate : There isn't any vertical acceleration !

-HvB99

 

[Dale]

You cannot express P in terms of T without some additional constraint information. For example, the condition that there is no vertical acceleration or something similar.

 

[hesher]

there is no paradox. you can't solve this problem with this method because T and P is not in same line. one vector can't generate a plane.the first one you don't consider the vertical force of T and the second one you don't consider sinx of P. if you want to express vectors, you need 2 vectors to describe the other one.

 

[HvB99]

You cannot express P in terms of T without some additional constraint information. For example, the condition that there is no vertical acceleration or something similar.

Yes...there isn't ...this was known...but i forgot to mention it...sorry!

 

[HvB99]

there is no paradox. you can't solve this problem with this method because T and P is not in same line. one vector can't generate a plane.the first one you don't consider the vertical force of T and the second one you don't consider sinx of P. if you want to express vectors, you need 2 vectors to describe the other one.

I'm sorry... but the other component...the one that isn't accounted for...as you said ...is the one causing a horizontal acceleration, since it is unbalanced( only that component ) ...

I merely equated the components of the two forces that were in the same direction.

 

[nasu]

How about the horizontal acceleration? What do you know about it?

By the way, with just these two forces you cannot have and equilibrium.
And it is good practice to state the problem completely before jumping to (or expecting) a "solution".

 

[Dale]

however T would have to be greater ...since its offsetting the downward vertical force of P and has a leftward horizontal component...

Given the additional information on the acceleration this is exactly correct. The vertical component of T is equal to P, and additionally T has a horizontal component that P does not.