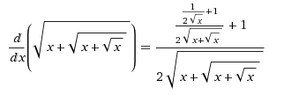Discussion Overview
The discussion revolves around finding the derivative of the function y=$\sqrt{x+\sqrt{x+\sqrt{x}}}$. Participants are exploring various methods for differentiation, including direct application of the chain rule and implicit differentiation. The context is primarily homework-related, with participants seeking assistance and verification of their approaches.
Discussion Character
- Homework-related, Mathematical reasoning, Technical explanation
Main Points Raised
- One participant presents their derivative calculation but receives feedback indicating a potential error in their placement of parentheses.
- Another participant suggests using implicit differentiation as a potentially easier method, providing a detailed step-by-step approach.
- A different method is proposed involving the substitution of a function g(x) to simplify the differentiation process.
- Participants express uncertainty about the correctness of their methods and seek confirmation or correction from others.
Areas of Agreement / Disagreement
There is no consensus on the correct method or final answer, as multiple approaches are presented and participants express uncertainty about their calculations.
Contextual Notes
Some participants' calculations depend on the correct placement of parentheses, and there are unresolved steps in the differentiation process. The discussion reflects various interpretations of the problem without a definitive resolution.
Who May Find This Useful
Students or individuals interested in calculus, particularly in differentiation techniques and resolving complex expressions involving nested functions.