You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Can Thales' Theorem Help Me Solve My Trapezoid Equation?
- Thread starter lornick
- Start date
-
- Tags
- Trapezoid
Mathematics news on Phys.org
MarkFL
Gold Member
MHB
- 13,284
- 12
I don't see an equation you are trying to complete, but what do we know about the opposite interior angles of a cyclic quadrilateral?
lornick
- 4
- 0
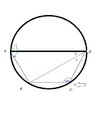
Sorry don't have an equation, my wording mistake, just trying to calculate the angle of E and F. What I have worked out is the angles of A, B, C, and D. A=70 B=110 C=120 D=60. But have no idea how to calculate E and F. If I turn C and D into a right angle on the outside of the trapezoid I get 30 and if I turn B and A into a right angle on the outside of the trapezoid I get 20. But not sure how to compute this into my E and F. Also I forgot to mention that A and D are parallel lines to B and C. Forgot to draw in the arrows on the line.Thank you for any help in solving this.
MarkFL
Gold Member
MHB
- 13,284
- 12
Since $\overline{AD}\parallel\overline{BC}$, and the trapezoid is cyclic, we know it must be isosceles. So we know $\angle A=60^{\circ}$, if $\measuredangle C=120^{\circ}$.
Thus, we know:
$$\angle E+\angle F=60^{\circ}$$
If we label the two angles at vertex $B$ as $G$ and $H$, we then know:
$$\angle G+\angle H=120^{\circ}$$
Can you find two more equations involving these 4 angles? Hint: add the interior angles of the two triangles making up the trapezoid...:D
Also, to simplify matters, $G$ and $H$ must share a special relationship to $E$ and $F$. ;)
Thus, we know:
$$\angle E+\angle F=60^{\circ}$$
If we label the two angles at vertex $B$ as $G$ and $H$, we then know:
$$\angle G+\angle H=120^{\circ}$$
Can you find two more equations involving these 4 angles? Hint: add the interior angles of the two triangles making up the trapezoid...:D
Also, to simplify matters, $G$ and $H$ must share a special relationship to $E$ and $F$. ;)
lornick
- 4
- 0
[QUOTE Since $\overline{AD}\parallel\overline{BC}$, and the trapezoid is cyclic, we know it must be isosceles. So we know $\angle A=60^{\circ}$, if $\measuredangle C=120^{\circ}$.
I had changed the original degrees and didn't realize I had changed the triangles to equal sides. My triangles are not level only the horizontal lines are level, which leaves me with one obtuse angle and one acute angle. :S so sorry I confused matters, but I didn't want to get into trouble for my question from my teachers. Or am I confused lol.
I had changed the original degrees and didn't realize I had changed the triangles to equal sides. My triangles are not level only the horizontal lines are level, which leaves me with one obtuse angle and one acute angle. :S so sorry I confused matters, but I didn't want to get into trouble for my question from my teachers. Or am I confused lol.
Last edited:
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
Hi lornick! Welcome to MHB! :)
Thales' theorem may help you.

Thales' theorem: if AC is a diameter, then the angle at B is a right angle.
Thales' theorem may help you.

Thales' theorem: if AC is a diameter, then the angle at B is a right angle.
lornick
- 4
- 0
I like Serena said:Hi lornick! Welcome to MHB! :)
Thales' theorem may help you.
Thales' theorem: if AC is a diameter, then the angle at B is a right angle.
Oh nooo I can't believe it was that simple, I have been trying to calculate it as a acute and obtuse angle (hence my issues). The time when you are doing maths and you start to bash your head against a brick wall, only to realize that the answer was right in front of you lol. Thank you sooooooooo much!
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 10
- Views
- 930
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 4K
- Replies
- 1
- Views
- 3K
- Replies
- 6
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 1K
Hot Threads
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
B How is it that law of sines does not work in this exercise?
- Started by mcastillo356
- Replies: 70
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math