jiaodaonline
- 5
- 0
Hi guys,
I got one confusion when reading Goldstein's Classical Mechanics (page 20, third edition). After getting the equation,
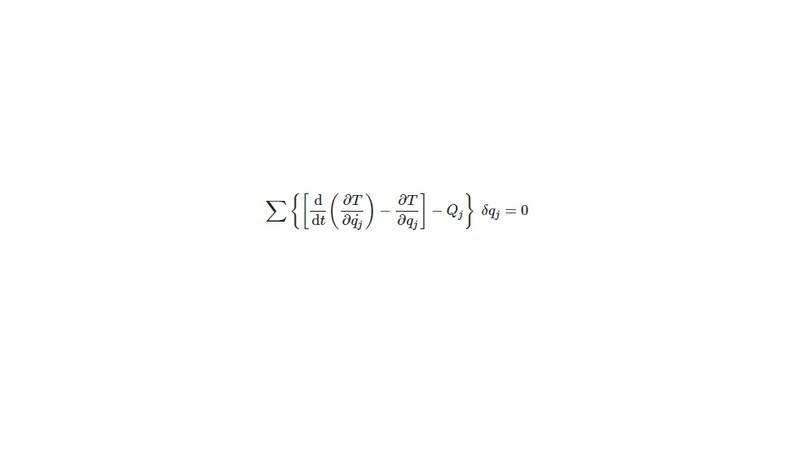
then it says that
Note that in a system of Cartesian coordinates the partial derivative of T with respect to qj vanishes. Thus, speaking in the language of differential geometry, this term arises from the curvature of the coordinates qj. In polar coordinates, e.g., it is in the partial derivative of T with respect to an angle coordinate that the centripetal acceleration term appears.
My question is: Is the above statement general, i.e., that the kinetic energy T does not depend on the position. I wonder why velocity can't depend on the particle's position vector. I mean, why couldn't we have cases where v(x, y, z, t), so that the kinetic energy depends on qj or r?
I got one confusion when reading Goldstein's Classical Mechanics (page 20, third edition). After getting the equation,
then it says that
Note that in a system of Cartesian coordinates the partial derivative of T with respect to qj vanishes. Thus, speaking in the language of differential geometry, this term arises from the curvature of the coordinates qj. In polar coordinates, e.g., it is in the partial derivative of T with respect to an angle coordinate that the centripetal acceleration term appears.
My question is: Is the above statement general, i.e., that the kinetic energy T does not depend on the position. I wonder why velocity can't depend on the particle's position vector. I mean, why couldn't we have cases where v(x, y, z, t), so that the kinetic energy depends on qj or r?