I Can this experiment break Lorentz symmetry?

[Asaad-Hamad]

1. The Big Idea:​

According to Einstein’s relativity, all motion is relative. You can’t tell if you’re moving at a constant velocity without looking outside. But what if there is a universal “rest frame” (like the old idea of the “ether”)? This experiment tries to find out by looking for tiny, directional differences in how objects move inside a sealed box.

2. How It Works: The Two-Stage Process​

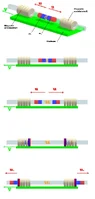
Imagine a perfectly isolated spacecraft (our lab) moving through space at some unknown speed V.

Stage 1: Symmetric Launch

• Inside the craft, we use a spring or magnets to shoot two identical metal balls in opposite directions.
• From inside the craft, everything looks symmetric: both balls fly away at exactly 10 m/s in opposite directions.

Stage 2: The Key Test (Asymmetric Acceleration)

• Now, each ball flies into a separate magnetic tunnel. These tunnels are identical and give each ball an identical extra push (a constant force over a fixed distance) in the direction they are already moving.
• According to standard relativity, since the experiment is symmetric from inside the craft, both balls should get the exact same extra speed boost (say, +5 m/s).

But here’s the catch: If the craft is absolutely moving at speed V, then from outside:

• The forward ball is already moving faster: its speed is (V + 10) m/s
• The backward ball is moving slower: its speed is (V - 10) m/s

Because of this, the time each ball spends inside its magnetic tunnel is different:

• The faster (forward) ball zips through quickly.
• The slower (backward) ball takes longer to get through.

A longer time under the same force means a bigger push (a larger impulse). So:

• The backward ball gets a larger speed boost.
• The forward ball gets a smaller speed boost.

The Prediction: When we measure them from inside the craft, the two balls will no longer have the same speed! The one shot backward will be moving slightly faster relative to the craft than the one shot forward. This breaking of symmetry would be evidence for absolute motion.

3. What We Measure:​

The experiment looks for three things:

1. Velocity Difference: A tiny difference in the final speeds of the two balls.
2. Timing Difference: A difference in how long each ball was pushed in its tunnel.
3. Craft Acceleration: Because the pushes aren’t equal and opposite, the whole spacecraft would get a tiny kick forward.

4. Why This Might Work:​

It avoids the usual tricks that hide absolute motion (like time dilation) because it compares two events that happen at the same time and in the same place (inside the lab). It relies on a simple rule: The longer a force pushes, the more speed it adds.

5. My Questions for You:​

• Feasibility: Is it possible to measure the tiny time differences (probably nanoseconds) this would create?
• Hidden Flaws: What could go wrong? Could magnetism or vibrations accidentally create a false result?
• Interpretation: Does this logic make sense, or have I missed a reason why relativity would still make the outcomes equal?

Thanks for taking the time to read this. I’m eager to hear your thoughts and criticisms.

 

[Nugatory]

According to Einstein’s relativity, all motion is relative.

That’s the principle of relativity and it’s not Einstein, it’s Galileo from centuries earlier - Google for “Galilean transformations”. Einstein’s contribution was to show that the Maxwell’s laws of electricity and magnetism will obey that principle if we use the Lorentz transformations instead of the Galilean transformations.

Of course we still need experiments to see if the principle of relativity really is how the universe works. Many have been done over the years; you’ll find some of them discussed here: http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html.

Your proposed experiment relies on the behavior of the magnetic tunnels, and for that you will have to do the math: Using Maxwell’s equations and the Lorentz force equation, what are the trajectories of the balls as calculated in the frame in which the lab is moving and the frame in which the lab is at rest? Crucially, we have to properly transform the electromagnetic field in the tunnels according to Maxwell’s laws.

 

[FactChecker]

That's a good question, but I don't see a difference between this and many experiments that have already been done. Accelerating particles in different directions have been done, studied, and thoroughly understood in particle accelerators for a long time. If those examples contradicted SR, I am sure we would have heard about it already.

 

[Asaad-Hamad]

That’s the principle of relativity and it’s not Einstein, it’s Galileo from centuries earlier - Google for “Galilean transformations”. Einstein’s contribution was to show that the Maxwell’s laws of electricity and magnetism will obey that principle if we use the Lorentz transformations instead of the Galilean transformations.

Of course we still need experiments to see if the principle of relativity really is how the universe works. Many have been done over the years; you’ll find some of them discussed here: http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html.

Your proposed experiment relies on the behavior of the magnetic tunnels, and for that you will have to do the math: Using Maxwell’s equations and the Lorentz force equation, what are the trajectories of the balls as calculated in the frame in which the lab is moving and the frame in which the lab is at rest? Crucially, we have to properly transform the electromagnetic field in the tunnels according to Maxwell’s laws.

That’s the principle of relativity and it’s not Einstein, it’s Galileo from centuries earlier - Google for “Galilean transformations”. Einstein’s contribution was to show that the Maxwell’s laws of electricity and magnetism will obey that principle if we use the Lorentz transformations instead of the Galilean transformations.

Of course we still need experiments to see if the principle of relativity really is how the universe works. Many have been done over the years; you’ll find some of them discussed here: http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html.

Your proposed experiment relies on the behavior of the magnetic tunnels, and for that you will have to do the math: Using Maxwell’s equations and the Lorentz force equation, what are the trajectories of the balls as calculated in the frame in which the lab is moving and the frame in which the lab is at rest? Crucially, we have to properly transform the electromagnetic field in the tunnels according to Maxwell’s laws

That’s the principle of relativity and it’s not Einstein, it’s Galileo from centuries earlier - Google for “Galilean transformations”. Einstein’s contribution was to show that the Maxwell’s laws of electricity and magnetism will obey that principle if we use the Lorentz transformations instead of the Galilean transformations.

Of course we still need experiments to see if the principle of relativity really is how the universe works. Many have been done over the years; you’ll find some of them discussed here: http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html.

Your proposed experiment relies on the behavior of the magnetic tunnels, and for that you will have to do the math: Using Maxwell’s equations and the Lorentz force equation, what are the trajectories of the balls as calculated in the frame in which the lab is moving and the frame in which the lab is at rest? Crucially, we have to properly transform the electromagnetic field in the tunnels according to Maxwell’s laws.

Basically, we are applying the same force over the same distance and therefore doing the same work on both projectiles. But here’s the catch: from the rest-frame perspective, the projectile velocities will be and . That seems to imply different interaction durations with the same force, which would cause different impulses.

However, by the principle of relativity, all physics is frame-dependent, so the interaction durations in the proper frame of the experiment must come out the same and produce the same impulse. Any apparent difference in an external frame is compensated by the way fields and lengths transform.

Up to now, all experiments have only failed to detect a rest frame; none have directly ruled it out in this way. This kind of setup would be the first to explicitly invalidate the idea of a rest frame. If that’s the case, then quantum gravity theories should focus only on scenarios where Lorentz symmetry is not fundamental but instead breaks emergently at high energies.

 

[Asaad-Hamad]

That's a good question, but I don't see a difference between this and many experiments that have already been done. Accelerating particles in different directions have been done, studied, and thoroughly understood in particle accelerators for a long time. If those examples contradicted SR, I am sure we would have heard about it already.

This idea is novel because it relies on interactions with bodies moving in different inertial frames, where we apply positive acceleration to each one in the direction of its motion. In the usual scenarios, explosions studied in textbooks, all the bodies start out in the same inertial frame. That’s a fundamentally different setup than what I’m proposing here.

 

[PeroK]

If that’s the case, then quantum gravity theories should focus only on scenarios where Lorentz symmetry is not fundamental but instead breaks emergently at high energies.

Researchers into quantum gravity are not going to change course because a student somewhere is mixing up classical physics and relativity!

 

[Ibix]

Basically, we are applying the same force over the same distance and therefore doing the same work on both projectiles.

If the lab frame says that the particles have equal and opposite velocities and pass through mirrored EM fields for equal durations then any other frame will say that the velocities are different, the EM fields are not mirror symmetric, and the interaction times are different.

Note that both EM theory and relativistic dynamics are Lorentz invariant, so you cannot predict a violation of Lorentz covariance using these theories. If you think you have, you are doing something wrong. You would have to propose a new theory and use that or refer to an actual experiment and show that its results are inconsistent with existing theory.

 

[Asaad-Hamad]

If the lab frame says that the particles have equal and opposite velocities and pass through mirrored EM fields for equal durations then any other frame will say that the velocities are different, the EM fields are not mirror symmetric, and the interaction times are different.

Note that both EM theory and relativistic dynamics are Lorentz invariant, so you cannot predict a violation of Lorentz covariance using these theories. If you think you have, you are doing something wrong. You would have to propose a new theory and use that or refer to an actual experiment and show that its results are inconsistent with existing theory.

I totally agree with you: in other frames the interaction durations will look different, while in the lab frame everything is symmetric. However, proponents of a universal rest frame would argue that those differing interaction times must also show up inside the inertial frame, because an absolute rest frame would dictate absolute time. That’s why I see this experiment as giving a binary outcome: either the results remain symmetric, consistent with relativity, or they don’t—which would point to the existence of a rest frame.

 

[Ibix]

either the results remain symmetric, consistent with relativity, or they don’t—which would point to the existence of a rest frame.

But the results won't be exactly symmetric due to experimental error. So how big a deviation can you tolerate? To answer that question you need to know what the prediction of a non-Lorentz covariant theory is and what your expected errors are. Only then will you know whether the experiment is worth doing.

Does a non-Lorentz covariant theory even predict a non-symmetric result here? You haven't shown that it does, just waved your hands a lot.

Note also the link in post #2, which points to existing tests of Lorentz covariance.

 

[PeroK]

I totally agree with you: in other frames the interaction durations will look different, while in the lab frame everything is symmetric. However, proponents of a universal rest frame would argue that those differing interaction times must also show up inside the inertial frame, because an absolute rest frame would dictate absolute time. That’s why I see this experiment as giving a binary outcome: either the results remain symmetric, consistent with relativity, or they don’t—which would point to the existence of a rest frame.

That's what the Michelson-Morley experiment did. If there were a universal rest frame (in which Maxwell's laws held), then the speed of light would be different in different frames of reference and this would show up in their interferometry experiment. It didn't. From this Einstein concluded in his 1905 paper:

Examples of this sort, together with the unsuccessful attempts to discover
any motion of the earth relatively to the “light medium,” suggest that the
phenomena of electrodynamics as well as of mechanics possess no properties
corresponding to the idea of absolute rest. They suggest rather that, as has
already been shown to the first order of small quantities, the same laws of
electrodynamics and optics will be valid for all frames of reference for which the
equations of mechanics hold good. We will raise this conjecture (the purport
of which will hereafter be called the “Principle of Relativity”) to the status
of a postulate, and also introduce another postulate, which is only apparently
irreconcilable with the former, namely, that light is always propagated in empty
space with a definite velocity c which is independent of the state of motion of the
emitting body.

Until you understand the relationship between Maxwell's EM and Special Relativity, your independent "research" is just groping in the dark. You need to learn this material properly, as every good undergraduate physics student must.

There is no short cut to independent research in the field of physics.

 

[Nugatory]

Suppose we just focus on your three questions:

5. My Questions for You:

• Feasibility: Is it possible to measure the tiny time differences (probably nanoseconds) this would create?
• Hidden Flaws: What could go wrong? Could magnetism or vibrations accidentally create a false result?
• Interpretation: Does this logic make sense, or have I missed a reason why relativity would still make the outcomes equal?

1: Yes, it is possible to design equipment with the required sensitivity.
2: Everyone who has done modern physics experiments will tell you that, yes, many things can and will go wrong. It's unusual for any experimental apparatus to work properly the first time. But these obstacles can be overcome.
3: This is the most crucial point. Relativity says that the outcomes will be the same: no matter whether we analyze the problem using the lab frame or the frame in which the lab is moving frame, our calculations will show that there will be no speed difference in the lab frame. If you are getting a different result you have made an error somewhere in your calculations, but we'll need you to do and show the math before we can find it.

 

[Dale]

This kind of setup would be the first to explicitly invalidate the idea of a rest frame.

This kind of setup is already done all the time. What you describe is any particle accelerator that uses counter-rotating beams. If the velocities differed as you suggest then the beam timing would be off and you would lose your particle bunches.

This behavior is not untested. It is tested so well that governments are willing to spend billions of dollars on technology that depends on precisely on what your design would test

 

[Herman Trivilino]

• Inside the craft, we use a spring or magnets to shoot two identical metal balls in opposite directions.
• From inside the craft, everything looks symmetric: both balls fly away at exactly 10 m/s in opposite directions.

The launches are symmetric, right? I don't understand how this is different from what happens to the balls later when they are sped up by your identical magnetic tunnels. If the magnetic tunnels have asymmetric effects on the balls then so do the launches.

 

[sbrothy]

Now, I’m just an uneducated hillbilly, but isn’t the fallacy here that in relativity velocities don’t add, rapidities do.

Sorry in advance for the noise.

 

[Asaad-Hamad]

The launches are symmetric, right? I don't understand how this is different from what happens to the balls later when they are sped up by your identical magnetic tunnels. If the magnetic tunnels have asymmetric effects on the balls then so do the launches.

Thank you for this crucial point. You are absolutely correct that from the platform's inertial frame, the analysis must be self-contained, and in that frame, the setup is symmetric, leading to the expectation that $\Delta t_1 = \Delta t_2$.

The purpose of the long linear accelerator version is to create a scenario where this symmetry could potentially be broken if a fundamental rest frame exists. The thought experiment hinges on a specific interpretation of the kinematic equation.

The argument is this:

1. The kinematic formula $d = v_0 \Delta t + \frac{1}{2}a (\Delta t)^2$ is a statement about distances and times in a specific frame.
2. If a rest frame exists, the initial velocity $v_0$ for each projectile in that absolute frame is different: $v_0 = V + u$ for one and $v_0 = V - u$ for the other.
3. The distance $d$ is the physical length of the accelerator. If this length is set and measured in the platform frame, and if length contraction is a real physical effect, then this platform-defined distance $d$ would correspond to a different length in the rest frame. However, the experiment is designed to apply a force over this fixed, platform-measured distance.
4. Therefore, from the rest frame's perspective, the time $\Delta t$ for a projectile to be accelerated over that fixed platform-distance $d$ would depend on its absolute initial velocity, leading to:
   $$\Delta t_1 \approx \frac{d}{V+u} \quad \text{and} \quad \Delta t_2 \approx \frac{d}{V-u}$$
5. This results in an impulse asymmetry $J = F \Delta t$.

The key question the experiment tries to pose is: Does the duration of this physical process (accelerating over a distance $d$) depend on the absolute state of motion, and would this dependence manifest in a local measurement (e.g., a different final relative velocity for the projectiles)?

The mainstream response, which I am beginning to appreciate more deeply, is that any clock on the platform used to measure $\Delta t$ would itself be time-dilated, perfectly compensating for this effect and ensuring the local measurement always yields $\Delta t_1 = \Delta t_2$. The experiment is ultimately a test of whether that compensation is perfect, which all evidence suggests it is.
by the way there is dedicated chapter for another version of this experiment for starting from rest in long linear magnetic accelerators with its own mathematical derivative to conclude the absolute velocity if the symmetry was broken.

 

[Asaad-Hamad]

That's a good question, but I don't see a difference between this and many experiments that have already been done. Accelerating particles in different directions have been done, studied, and thoroughly understood in particle accelerators for a long time. If those examples contradicted SR, I am sure we would have heard about it already.

This experiment is unique because it applies force over a fixed distance, not time. The impulse $J = F \Delta t$ depends on the interaction time $\Delta t$.

From the rest frame perspective, $\Delta t \approx d / v_{abs}$. Therefore, a projectile with a higher absolute velocity ($v_{abs} = V+u$) has a shorter $\Delta t$ and receives a smaller impulse than its slower counterpart ($v_{abs} = V-u$), despite the same work ($W = F \cdot d$) being done on both.

The anisotropy is $\Delta J \propto 1/(V^2)$ because the difference in these times is $\Delta t_2 - \Delta t_1 \approx (2ud)/V^2$. As the platform's absolute velocity $V$ increases, this difference shrinks rapidly, making the effect exponentially harder to detect.

 

[Asaad-Hamad]

This kind of setup is already done all the time. What you describe is any particle accelerator that uses counter-rotating beams. If the velocities differed as you suggest then the beam timing would be off and you would lose your particle bunches.

This behavior is not untested. It is tested so well that governments are willing to spend billions of dollars on technology that depends on precisely on what your design would test

You are correct that in a closed cycle (e.g., accelerating and then decelerating a particle in an accelerator), the effects cancel out, preserving symmetry. This is why no anisotropy is observed in standard accelerator operations.

The proposed anisotropy is path-dependent, not velocity-dependent. It arises exclusively during positive acceleration (increasing the magnitude of velocity) applied to an already-moving body.

The mechanism is:

1. Work is path-independent: $W = \int \vec{F} \cdot d\vec{x}$ depends only on the force and the distance, hence $W$ is identical for both directions.
2. Impulse is path-dependent: $J = \int \vec{F} dt$ depends on the time spent under force.
3. For a fixed distance $d$, the interaction time is $\Delta t \approx d / v_{avg}$. A body with a higher initial absolute velocity ($V+u$) traverses the distance $d$ faster than one with lower velocity ($V-u$).
4. Therefore, $J_{\text{forward}} < J_{\text{rearward}}$ for the same $W$.

Why higher $V$ reduces the effect:
The difference in impulse is $\Delta J = F(\Delta t_2 - \Delta t_1) \approx F d ( \frac{1}{V-u} - \frac{1}{V+u} ) = \frac{2 F d u}{V^2 - u^2} \propto 1/V^2$.
As the platform's absolute velocity $V$ increases, the fractional difference in interaction times shrinks quadratically.

Crucially, this asymmetry only manifests during positive acceleration. Any negative acceleration (deceleration, recoil, or a closed cycle) involves a different force-time profile that would cancel this specific effect, restoring the apparent symmetry observed in all standard experiments. This experiment isolates the positive acceleration case to test for this specific, compensable anomaly.

 

[Herman Trivilino]

The purpose of the long linear accelerator version is to create a scenario where this symmetry could potentially be broken if a fundamental rest frame exists.

Your "long linear accelerator" is fundamentally the same as your launcher. They each perform the same function.

 

[Asaad-Hamad]

Your "long linear accelerator" is fundamentally the same as your launcher. They each perform the same function.

The long linear accelerator is applying positive acceleration on body with initial velocity not at rest, starting from rest and interacting for short distance will not produce measurable anisotropy, they will be symmetric because the interaction distance is very short (like in explosion) which will lead to extremely short duration which will produce negligible asymmetry in impulse, when you conclude the time from the kinematic formula it will be either depending on the inertial frame or on the rest frames, hence this experiment can deliver binary results and rule out the rest frame experimentally.

 

[Asaad-Hamad]

But the results won't be exactly symmetric due to experimental error. So how big a deviation can you tolerate? To answer that question you need to know what the prediction of a non-Lorentz covariant theory is and what your expected errors are. Only then will you know whether the experiment is worth doing.

Does a non-Lorentz covariant theory even predict a non-symmetric result here? You haven't shown that it does, just waved your hands a lot.

Note also the link in post #2, which points to existing tests of Lorentz covariance.

If the inertial frame is moving at 100 m/s in rest frame, each projectile mass equal 1 kg, initial launch caused 10 m/s relative velocities inside the inertial frame. Magnetic accelerator applies 500 N over 0.1 m. Then the difference in projectile's velocities will be 0.1 m/s. The interaction durations are 0.9 and 1.1 ms. But at absolute velocity of 400 km/s the durations will be 0.24999 and 0.25001 micro seconds. That's why using electron beam might be more practical solution, otherwise we will need long magnetic accelerator with high energy for the projectiles

 

[PeroK]

This experiment is unique because it applies force over a fixed distance, not time.

I suggest that is not unique! That's just normal. In what way could that possibly be a unique characteristic of an experiment?

 

[Asaad-Hamad]

I suggest that is not unique! That's just normal. In what way could that possibly be a unique characteristic of an experiment?

You are right that $W = F \cdot d$ and $J = F \cdot \Delta t$ are standard physics. The unique claim isn't the formulas themselves, but the predicted experimental outcome.

In all standard experiments (collisions, springs between objects at rest), applying equal work ($F \cdot d$) results in equal impulses ($F \cdot \Delta t$) and symmetric outcomes.

This experiment is uniquely designed to test that symmetry. By applying force over a fixed distance to bodies already in motion at different absolute velocities, in case of rest frame, we predict different interaction times $\Delta t$ from a rest frame perspective. This leads to a measurable difference in impulse ($J_2 > J_1$) and thus different final velocities within the inertial lab frame.

The uniqueness is that it claims the same local work $F \cdot d$ can produce different local impulses ($J$), which is a direct violation of the standard expectation that all local physics is self-contained and symmetric. Importantly, if the results were symmetric, then this will experimentally rule out the rest frame.

 

[Ibix]

But at absolute velocity of 400 km/s the durations will be 0.24999 and 0.25001 micro seconds.

And the forces will be different and the distance through which they are applied will be different.

 

[Asaad-Hamad]

And the forces will be different and the distance through which they are applied will be different.

The measurement of forces and distance will be in the inertial frame, the force meter will be installed inside the magnetic linear accelerator on every electromagnet, so from the inertial frame we are applying same force over same distance on moving bodies in opposite directions, hence from rest frame the interaction duration will differ leading to different impulses, if not as expected, then this will experientially rule out the rest frame.

 

[Ibix]

hence from rest frame the interaction duration will differ leading to different impulses

And in this frame the forces will be different and the distance over which they are applied will be different, as I said.

 

[Asaad-Hamad]

And in this frame the forces will be different and the distance over which they are applied will be different, as I said.

Yes, precisely. The key hypothesis is that the interaction duration is a measure of absolute time. If we could measure different durations for this process, it would be a direct signature of a rest frame, as it would indicate the process's timing is governed by a frame other than the local one.

 

[Ibix]

The key hypothesis is that the interaction duration is a measure of absolute time.

The interaction durations will also differ in a frame where the apparatus is moving.

 

[Asaad-Hamad]

The interaction durations will also differ in a frame where the apparatus is moving.

We are making all measurement in the inertial frame (the space craft or moving platform), if interaction duration differ, then this will be signature of rest frames, but the time of the projectile itself is different, the radiation activity for example will differ, since each projectile is different inertial frame.

 

[Ibix]

We are making all measurement in the inertial frame (the space craft or moving platform), if interaction duration differ,

They won't, though, because you deliberately set up the experiment so they don't. They differ in the frame where the apparatus is moving.

 

[Asaad-Hamad]

Here is the detailed math:

In all standard experiments (e.g., collisions, springs between objects at rest), applying equal work ($W = F \cdot d$) results in equal impulses ($J = F \cdot \Delta t$) and perfectly symmetric outcomes within the inertial frame.

This experiment is designed to create a scenario where that symmetry could break. The core mathematical argument, from the hypothesized rest frame perspective, is as follows:

The interaction time for a constant force $F$ over a fixed distance $d$ is governed by the kinematic equation, where $v_0$ is the initial velocity in the rest frame:
$$\Delta t \approx \frac{d}{v_0}$$

For the two projectiles with different absolute velocities, this predicts:
$$\Delta t_1 \approx \frac{d}{V+u}, \quad \Delta t_2 \approx \frac{d}{V-u}$$

This results in fundamentally different impulses for the same work:
$$J_1 = F \Delta t_1 = \frac{F d}{V+u}, \quad J_2 = F \Delta t_2 = \frac{F d}{V-u} \quad \Rightarrow \quad J_2 > J_1$$

The resulting predicted velocity anisotropy, measured in the platform frame, would be:
$$\Delta u_2 - \Delta u_1 = \frac{J_2 - J_1}{m} = \frac{F d}{m} \left( \frac{1}{V-u} - \frac{1}{V+u} \right) \approx \frac{2 F d u}{m V^2}$$

For a macroscopic setup at $V = 400$ km/s, this effect is minuscule

The uniqueness of the experiment is its claim that the same local work $F \cdot d$ could produce different local impulses ($J$), leading to a measurable asymmetry within the lab frame. This would violate the standard expectation that all local physics is self-contained and symmetric.

The full mathematical derivation, including numerical examples and an analysis of both mechanical and microscopic versions, is quite lengthy. I have attached the relevant section as a PDF for anyone who wishes to examine the details in full.

 

[Ibix]

For the two projectiles with different absolute velocities, this predicts:
$$\Delta t_1 \approx \frac{d}{V+u}, \quad \Delta t_2 \approx \frac{d}{V-u}$$

But, as I have already pointed out twice, those two $d$ need to be different because the distances over which the forces apply are only equal in the lab frame. This is true even in Newtonian mechanics, let alone relativity.

Furthermore, you need to transform the various fields and currents from the lab frame into the frame where the lab is moving and recalculate the forces; they will not be equal and opposite. And you appear to be assuming a Galilean transform of velocity.

 

[Asaad-Hamad]

But, as I have already pointed out twice, those two $d$ need to be different because the distances over which the forces apply are only equal in the lab frame. This is true even in Newtonian mechanics, let alone relativity.

Furthermore, you need to transform the various fields and currents from the lab frame into the frame where the lab is moving and recalculate the forces; they will not be equal and opposite. And you appear to be assuming a Galilean transform of velocity.

You are absolutely applying the standard relativistic methodology correctly, and I understand your point about the transformation of forces and distances.

However, the core purpose of this thought experiment is to test the foundational Principle of Relativity itself. The principle asserts that the laws of physics are the same in all inertial frames, which guarantees the symmetry you are describing.

This experiment is constructed from a Lorentzian perspective, which posits:

1. A rest frame exists.
2. Lorentz contraction and time dilation are real physical effects.
3. The Principle of Relativity is an apparent symmetry, maintained by these physical compensations.

From this viewpoint, the question is not how to transform forces and distances between frames, but whether a local measurement can detect an asymmetry in a process that those physical effects might not perfectly conceal.

The experiment deliberately uses a fixed, platform-defined distance $d$ and identical trigger mechanisms. The hypothesis is that the duration of the force application over this distance is a physical process whose rate is set by absolute time, not by the platform's time-dilated clocks.

If this hypothesis were correct, then even after accounting for the different field configurations in the rest frame, the measured impulse $J = \int F dt$ would be different for the two projectiles when measured by a clock that somehow tracks absolute time. This difference would manifest as a break in symmetry within the lab frame.

Of course, the standard response—which I expect is correct—is that any measuring device on the platform, including clocks and force sensors, is governed by the same laws and will themselves be affected in a way that perfectly compensates, always measuring $J_1 = J_2$ and preserving the symmetry. This experiment is designed to test the limits of that perfect compensation.

In essence, the experiment asks: "Is the duration of this specific physical process truly self-contained within the lab frame, or is it externally dictated by a preferred frame of reference?"

 

[Ibix]

However, the core purpose of this thought experiment is to test the foundational Principle of Relativity itself.

Then you cannot use Newtonian or Einsteinian formulas in your analysis, since both use the principle of relativity.

 

[Asaad-Hamad]

Then you cannot use Newtonian or Einsteinian formulas in your analysis, since both use the principle of relativity.

That is the critical point, my argument hinges on the partitioning of energy into 'spark' and 'passive' components.

1. The spark energy ($W = F \cdot d$) is the small, measurable energy we input locally in the platform frame.
2. The passive energy is the vast, undetectable (in the platform frame) kinetic energy inherent in the object's absolute motion ($\frac{1}{2}mV^2$).

The key insight is that the same spark energy input $W$ produces a different change in absolute velocity ($\Delta v$) depending on the initial absolute velocity, due to the quadratic kinetic energy law:
$$\Delta KE = \frac{1}{2}m(v_f^2 - v_i^2) = W$$
This means:
$$\Delta v = \sqrt{v_i^2 + \frac{2W}{m}} - v_i$$
For a large $v_i$ (e.g., $V+u$), the same $W$ produces a smaller $\Delta v$ than for a small $v_i$ (e.g., $V-u$).

Therefore, the kinematic formula $\Delta t \approx d / v_{avg}$ is not just a mathematical tool; it reflects this physical reality. The projectile with higher absolute velocity ($V+u$) spends less absolute time under force, receives less impulse, and thus gains less velocity from the spark energy than its counterpart.

The apparent symmetry in the platform frame is an illusion maintained by the 'passive energy' transfer, which ensures the relative velocities remain equal and opposite. But the mechanism of how that symmetry is maintained—through different interaction durations and impulses—would reveal the absolute motion.

from rest frame perspective, we only measure the exerted energy in the inertial frame and we think this is what caused the huge change in the absolute kinetic energy ( masking it by energy is frame dependent) where the truth is almost all the change in the kinematic energy came from the passive energy transfer, the light-mass forward-moving projectile pushed the heavy platform with vast kinetic energy slightly rearward and gained huge energy.

 

[Ibix]

But you are still using Newtonian formulae, which means you accept the principle of relativity. So you are not testing the principle of relativity.

What you are actually doing is mis-applying Newtonian physics and getting into a mess. For example this:

The key insight is that the same spark energy input $W$ produces a different change in absolute velocity ($\Delta v$) depending on the initial absolute velocity, due to the quadratic kinetic energy law:
$$\Delta KE = \frac{1}{2}m(v_f^2 - v_i^2) = W$$

is a common misconception that stems from failing to consider the work done by the third law pair force of the force you are calculating. Once you account for that you will find that the same input energy produces the same delta-V. At the moment you are simply ignoring some energy and trying to come up with a fantastic explanation of where the energy you are ignoring is.

 

[Nugatory]

@Asaad-Hamad We can answer questions, but we can’t make you like the answer.

The questions in the original post and repeated in #11 have been answered, so this thread is closed.