paawansharmas
- 19
- 0
My doubt is that whether we can apply non-linear smoothing to a almost linear data ( without one or 2 discontinuity)
I have attached the pic in which the red data is the smoothed one. Blue is the original one.
I multiplied each point with an increasing like 1, 1.1, 1.2, 1.3, 1.4...so on
My question is : is this valid way to remove discontinuity or to make a linear correlation stronger ??
thanks
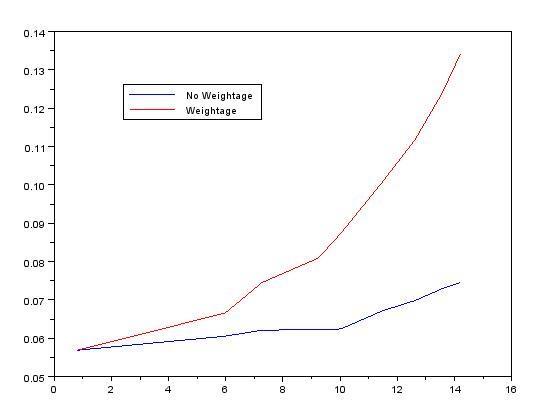
I have attached the pic in which the red data is the smoothed one. Blue is the original one.
I multiplied each point with an increasing like 1, 1.1, 1.2, 1.3, 1.4...so on
My question is : is this valid way to remove discontinuity or to make a linear correlation stronger ??
thanks
