Can we write Rolle's Theorem this way?

[nil1996]

Rolle's theorem:

Statements:
If y =f(x) is a real valued function of a real variable such that:

1) f(x) is continuous on [a,b]
2) f(x) is differentiable on (a,b)
3) f(a) = f(b)

then there exists a real number c$\in$(a,b) such that f'(c)=0

what if the the f(x) is like the following graph:

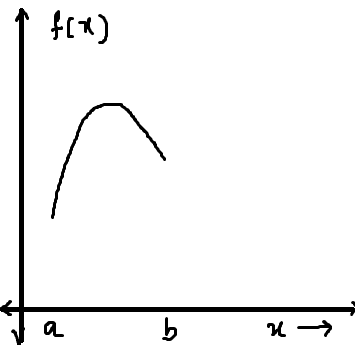
here there is a point 'c' for which f'(c) =0 but f(a) $\neq$ f(b)

So to take such cases in consideration can we make a change to the last statement of Rolle's theorem as:
3)f(c) > [f(a),f(b)] Or f(c)<[f(a),f(b)]

are there any exceptions to the above statement?

 

[Office_Shredder]

Yes, that statement works. The easiest way to prove this is to notice that if f(c.) > f(b) > f(a) (for example), then there exists some d such that a<d<c and f(d) = f(b) by the intermediate value theorem. Then applying Rolle's theorem to the interval [d,c] completes the proof.

This computer seems to insist on writing f(c.) without the period as f©, hence the strange notation.

 

[nil1996]

Then applying Rolle's theorem to the interval [d,c] completes the proof.

Do you mean interval[d,b]

 

[Office_Shredder]

Yeah good catch

 

[nil1996]

Thanks