Can Weight Transfer Cause a Car to Stay in a Stuck Position?

[at570]

I have a rather unusual problem and I want to understand the physics of it.
Imagine a car with a high center of gravity and front and back wheels close together.
It gets some speed and then brakes, and the front goes down.Just when it stops, and the load tranfer is done, there's no force from braking pushing the front down, only weight transfer from the center of gravity moving, specifically a line from the center of gravity straight down to the ground moving closer to the front wheels because of the rotation of the body, putting more of the cars weight on the front two wheels.
Is there ever a situation where it will stay in this position? It has springs and dampers on all 4 wheels and there's no damage. Also don't include fluids shifting due to inertia in weight transfer. What equations talk about this? Why do cars generally right themselves and return to level and not some other angle based on the center of gravity and the 4 spring forces?

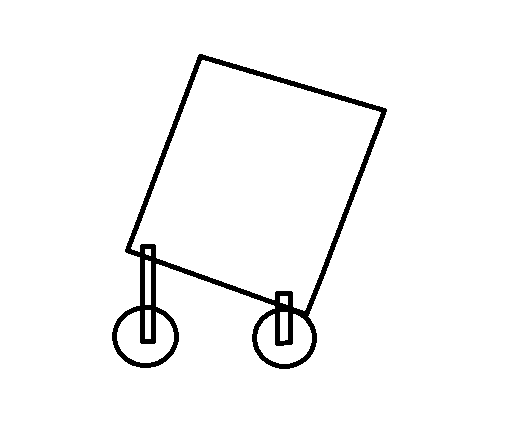
Heres a picture of the car and the position it could get stuck in.
I see 3 main things that would effect whether or not the car will do this, spring force or spring constant, center of gravity location, and distance between the front and back wheels. Basically, what equations talk about weight transfer overcoming the spring force? Can you possibly find the spring force or spring constant that is the threshold where this will start to happen? Or some other way? Please use equations. I think this has to do with spring systems. How would you go about solving this? What physics ideas would you use? I am really not sure how to come at this problem. Also, the springs are all the same, and the wheels are equal distance from the center of gravity when its vertical. Thanks

 

[mfb]

Only if the car is built that way, or if something goes wrong. Otherwise the regular orientation is the only equilibrium position. Cars are designed that way - the springs have to be strong enough to lift the front up again.

 

[at570]

So, when cars are designed is there a certain force the springs have to have so this can't happen? If I understand it right, if you built a car and it did this it would mean the springs are too weak then?

 

[mfb]

I don't see a situation where this would be a realistic danger. You would need extremely long and weak springs. It wouldn't look like a car, it would look like some weird piece of art.

 

[Bystander]

Google "what is a toggle mechanism."

 

[at570]

Im thinking mabey a bus turning side to side so it would be left to right instead of front to back, or an offroad vehicle. So, if the car did that the springs I think would be strong enough so it doesn't bottom out all 4 wheels, but not strong enough to return it to level? Can anyone confirm this? But if you wanted to figure out the minimum force for the springs to have for it to not do this on the hypothetical car, how would you do it? I am thinking mabey find the most weight the front wheels would have to carry and the spring force would have to be at least equal to that? I also looked up toggle mechanism and I see that its used in suspensions. I also think you could use the mechanical advantage balance to figure out how much weight is on each wheel?

 

[at570]

I like air suspensions

 

[at570]

Can someone check my physics on this? I am going to use the largest angle down it can get with the front spring compressed all the way.
Im going to do distance from the center of gravity to the front wheels / distance between the wheels = weight on the front wheels
convert from kg to n and divide by 2 wheels = minimum spring force to keep this from happening
Im wondering if the spring force is strong enough to push it up at the farthest angle down, will it be stronger than the weight the entire way back? As the spring gets longer the force will decrease and as the body rotates back the weight on the front wheels will also decrease. If I use the farthest angle it could be at, does that mean there won't be a point where the weight will be stronger than the spring force and it will settle there? Mabey you can solve this with energy? If you use energy for the body do you need to use the energy to raise the center of gravity and the energy to rotate it?

 

[Wes Tausend]

When the load is centered back over the chassis, the springs largely return to their original state because when the front springs are decompressed they push the front back up (in your case). This happens the same way as a bathroom scale returns to zero when one steps back off of it. One thing to note is that steel springs do this return the best since they have a very linear travel length, directly proportional to weight. Rubber doesn't return as well as an example, and tires struggle to 'unflatten' once they pass bottom, even at speed. That is because tires have a sort of internal friction that also makes them hot because of this flexing. The internal friction thus damps the rebound of rubber which makes it a naturally damped spring for softness and vibration absorption. Thus bodies and some spring mounts are cushioned with rubber for extra comfort (until the rubber ages from heat cycles and hardens).

Steel springs on the other hand pretty much rebound fully, rapidly and stay cool which is why they have shock absorbers (American term) attached to them. The spring rebound would be about as violent as the original nasty bump in a merely delayed bounce otherwise. To dissipate that unwanted road-jolt energy, the shock absorbers add friction to the suspension travel to steal bounce energy. They mostly damp the rebound which is why Britain calls them "dampers" (which is probably a more accurate nomenclature). The shock piston drags through internal oil to provide friction which is why they actually get hot on rough roads. There is a small hole arrangement in the piston to allow leakage to allow the shock to move at all or it would be totally hydraulically locked solid instead of partially and moving slow.

Since it is possible to use separate holes with one-way valves to adjust the damping for compression vs. rebound, the shocks are often adjusted to 70% rebound friction and 30% compression friction. As you might well guess, at 70%, the suspension doesn't rebound as fast and this fact can actually cause the suspension to pump itself temporarily lower in the case of a series of stutter bumps. For this same reason there is a slight temporary sag from the shocks from the stop you mentioned, but there is also a remaining sag because of other true constant friction in suspension movement. It's called stiction. It's not very much but you can sit on the front fender of your car, get back off gently so as to not bounce it and measure a slight sag as opposed to allowing a quick bounce where the car is likely to center more upright on all the springs.

When the car is left stuck in a sag after a stop, there is also a slight static weight transfer that helps it stay that way. So in effect, the car does stay slightly in a stuck position after braking... just like you thought. It just isn't very much.

The idea that automotive steel springs are largely all the same (the same old nearly perfected alloy actually) will allow you to calculate the suspension travel vs. load easily once you find the formulas and weigh each wheel. Or you can do it by experiment which is better anyway. Just add weight above each wheel and measure the compression (fender lip to ground). Engineers usually calculate suspension travel, or work off a spring-rate table because they do watch weight very closely since fuel economy concerns and they know that. But they always end up actually measuring it too, to be sure. Gotta end up with that cool stance so the car looks fast even when it's standing still, right?

Wes

 

[russ_watters]

So, if the car did that the springs I think would be strong enough so it doesn't bottom out all 4 wheels, but not strong enough to return it to level? Can anyone confirm this?

If you are asking whether the weight transfer can ever be enough to create a new stable point, it is still no: springs are linear force devices, meaning the force is proportional to the distance traveled. And if it is a deceleration causing the weight transfer, when the deceleration stops, the extra force of the deceleration goes away. So it has to spring back.

 

[sophiecentaur]

As the spring gets longer the force will decrease and as the body rotates back the weight on the front wheels will also decrease.

This is the basis of why the picture is an unlikely event. Any further displacement will increase the force from the spring under the lower part of the car and decrease the force on the higher part. This will tend to RESTORE the angle to horizontal.
Of course, there is nothing to stop some daft young man from putting rams on his suspension to lift the front or back independently. I do wonder about the legality of that but you do see pictures . . . . . . . .
PS I say "young man" for obvious reasons; the observed relative maturity of young men and young women, for one.

 

[Wes Tausend]

All of the OP's thoughts seem to mix practical physics (practical engineering really) with ideal physics. I believe this leads to his (or her) confusion.

Ideal physics follows certain black and white laws, believed immutable, that when finally broken, generally form new, better immutable laws. Meanwhile we use the supposed immutable laws we have. One such currently immutable law dealing with springs is Hooke's law. If the OP really wants to know about springs and formulas, he (or she) will have to learn about physics until he understands Hooke's law.

Then, when he becomes one of our finest automotive engineers (and the curious, obsessive sort do) he will find out about all the gray areas where other forces creep in and ruin perfectly good master-plans built upon the better known immutable laws. Original component specifications pretty much all have to be improved by some additional tinkering that is derived by pure (and fun) detective work... on a test track. Hardly anything works right out of the box... er off the drawing table. If the perfectly law-compliant auto is ever designed and is perfectly describable, the autos will soon all be alike and all automotive engineers will be out of a job. No worry though. Murphy's law rules all others.

I thought it worthy to point out in post #9 that machinery, such as auto suspension, does not seem to perfectly obey laws we are pretty sure are immutable. In the case of auto suspension, sneaky joint friction is usually the main culprit. To be totally honest, a car sometimes does remain in a very slightly unlevel condition after stopping. But agreed, it's not a major failure of Hooke's law like we strongly suspect the OP suspected.

Story:
I once got into a discussion with another gentleman about truck tires, the smaller type truck used to pull RV campers. The other fellow felt that slightly larger tires could offer no improvement in dry traction because, in class, we all learned that friction is directly related to force, in this case a constant gravity force holding the high-friction tire contact area against the pavement.
Consider the three empirical laws of dry friction for example:

• Amontons' First Law The force of friction is directly proportional to the applied load.
• Amontons' Second Law: The force of friction is independent of the apparent area of contact.
• Coulomb's Law of Friction: Kinetic friction is independent of the sliding velocity.

By simple physics, a smaller tire "footprint" should theoretically concentrate the force and logically develop the precise increase of a proportionate identical traction. But it doesn't.

The tire traction discussion was concerned mostly with turning and stopping where the weight is shifted just as our OP described in his first post. The problem is there are some difficult-to-calculate forces, such as adhesion of dissimilar materials, that can modify this in a spooky non-linear fashion. One might think that, according to ideal physics, as weight came off the rear tires in a stop, or inside tires in a turn, that the other tires would, by law, gain equal weight and make up for this loss phenomena with the subsequent development of proportionate greater force per square inch against the pavement. They don't.

It turns out the ideal tire traction is to keep equal weight on all tires. When one or more wheels lighten their load because of effective load shift, the overall traction is reduced in spite of the fact that the other more loaded tires have a proportionate increase in force (but not traction). And that is why wide tires are used for racing on pavement. For dry traction, the wider the better; but for aerodynamics and frictional rotation drag, not so much. The racing traction compromise is still largely an art and competition is where the good stuff comes from.

Wes
~

 

[sophiecentaur]

All of the OP's thoughts seem to mix practical physics (practical engineering really) with ideal physics. I believe this leads to his (or her) confusion.

This is true of many of the posts on PF. It may not be just the way the OP is posed; the confusion is often introduced by someone later trying to be 'helpful'. (Other times it can just be someone attempting to be too smart, but we have all been there)
Motor cars are the worst case of non-ideal performers yet they are so frequently introduced into discussions about Physics. Perhaps they should be 'banned' (or a Congestion Charge applied, as in central London, where there are just too many of them! )

 

[Dr. Courtney]

Amontons' First Law The force of friction is directly proportional to the applied load.
Amontons' Second Law: The force of friction is independent of the apparent area of contact.
Coulomb's Law of Friction: Kinetic friction is independent of the sliding velocity.

It's hard for me to regard these as laws, in the usual sense - they are more like useful first order approximations.

Sure, in simple scenarios, they are good to 10% or so in introductory physics labs as long as the independent variable only changes by a factor of 2-5ish. But go changing the applied load, the contact area, or the sliding velocity by a factor of 10-100 and go measuring the frictional force to an accuracy of 1% and you are much less likely to find experimental agreement with these "laws."

 

[Wes Tausend]

This is true of many of the posts on PF. It may not be just the way the OP is posed; the confusion is often introduced by someone later trying to be 'helpful'. (Other times it can just be someone attempting to be too smart, but we have all been there)
Motor cars are the worst case of non-ideal performers yet they are so frequently introduced into discussions about Physics. Perhaps they should be 'banned' (or a Congestion Charge applied, as in central London, where there are just too many of them! )

Guilty as charged. .. And often half the businesses on our streets have to do with motorcar accessories. Thanks for commenting.
Wes

It's hard for me to regard these as laws, in the usual sense - they are more like useful first order approximations.

Sure, in simple scenarios, they are good to 10% or so in introductory physics labs as long as the independent variable only changes by a factor of 2-5ish. But go changing the applied load, the contact area, or the sliding velocity by a factor of 10-100 and go measuring the frictional force to an accuracy of 1% and you are much less likely to find experimental agreement with these "laws."

Part of the point for my discussion with the other gent. Very "mutable" approximations that would be better listed as "Rules of Thumb". But sometimes even the best laid of them crumble (rather rarely at least ). Thanks for commenting.
Wes