Challenge Can You Solve These Math Challenges?

[StoneTemplePython]

Solution to #3
The average win for heads or tails is 2 with probability 4/5.
A risk neutral player will play as long as her expectation is positive. She will quit if her expectation is ≤ 0.
If she has accrued x, then her expectation for the next play 2⋅4/5 - x⋅1/5. That is positive for x < 8 and ≤ 0 for x for x ≥ 8.
Thus she will quit when x ≥ 8, assuming "other" has not occurred.

We must now determine the expected value of that strategy. Let p = 2/5.
If she gets to x = 7, then with prob 2p her expected win will be 9.
There are various ways to get to x= 7,
by 7 1's with prob p⁷, or
by 4 1's and a 3 with prob 5⋅p⁵, or
by 2 3's and a 1 with prob 3⋅p³.
Thus the expected win win via x = 7 is (p⁷ 2p + 5p⁵ 2p + 3p³2p)9.

She can also win by having x = 6 and getting a 3, and there are various ways to get x = 6,
by 6 1's with prob p⁶, or
by 3 1's and a 3 with prob 4p⁴, or
by 2 3's with prob p².
Each of these pay 9 with total prob = p⁷ + 4p⁵ + p³.

Finally, she can also win by having x = 5 and getting a 3. There are 2 ways of getting x = 5,
by 5 1's with prob p⁵, or
by 2 1's and a 3 with prob 3p³.
Each of these pay 8 with total prob = p⁶ + 3p⁴.

Adding the three cases we get the expected win to be 3.37 which is what a neutral player should pay.

Nicely done.

For the benefit of other readers, I'd belabor the point that you first came up with a stopping rule: to stop when the expected value is no longer positive.

The expected cost of playing another round goes up in proportion to your current stake -- specifically the proportion is $\frac{1}{5}$. On the other hand the expected benefit of another play is constant. Hence there is a single point of interest -- the maximum -- which you found at $8$.
- - - -
Part 2 then is figuring out the expected value, now that you have the stopping rule in place. Your careful approach is how -- I imagine-- Fermat would solve the problem.
- - - - - - - - - - - - - - - - - - - -
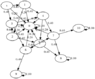
It may help some people to see a state diagram of the process to work through those path probabilities. I've dropped this in below.

There is a dummy state 's' which denotes the starting state. All other node labels correspond the stake value at that state. This should be mostly interpretable, though the software I use is a bit clunky at times, e.g. with respect to node 5.

- - - -
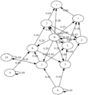
And if one is thinking about the process in reverse -- i.e. (expected values probabilistically) flowing back to state 's', people may want to consider the reversed stated diagram, below.

 

[Zafa Pi]

Part 2 then is figuring out the expected value, now that you have the stopping rule in place. Your careful approach is how -- I imagine-- Fermat would solve the problem.

I have a picture of Fermat and he talks to me, so I can't take full credit.

optional:
How many rounds would it take on average for the game to terminate? (You may assume a mild preference for shorter vs longer games in the event of any tie breaking concerns.)

Now suppose the player doesn't care about the score and just loves flipping coins -- how long will the game take to terminate, on average, in this case? \space (by @StoneTemplePython)

Solution to optional:
The expected number of rounds for the game to terminate = ∑n⋅prob game ends on nth round, n ∈ [1,8] (see post #60).
Prob game ends on nth round = prob "other" is rolled at the nth turn + prob game terminates by a win at the nth roll.
Let p = ⅖.

Round)
1) ⅕ + 0
2) (either a 1 or a 3) 2p⋅⅕ + 0
3) (either 1&1, or 1&3, or ...) 4p²⅕ + (3 3s) p³
4) (no 3s) p³ ⅕ + (1 3 & 2 1s) 3p³⅕ + (2 3s & 1 1) 3p³⅕ + (2 3s & a 1 then any) 6p⁴
5) (no 3s) p⁴⅕ + (1 3 & 3 1s) 4p⁴⅕ + (3 1s & 3 then 3) 4p⁵
6) (no 3s) p⁵⅕ + (1 3 & 4 1s) 5p⁵⅕ + (4 1s & 3 then any) 10p⁶ + (5 1s then 3) p⁶
7) (no 3s) p⁶⅕ + (6 1s then 3) p⁷
8) (no 3s) p⁷⅕ + (7 1s then any) 2p⁸
Now multiply the round by its total prob and add them up to get about 2.8 expected rounds.

If she just keeps on flipping regardless of score the expected number of rounds = ∑n⋅⅘^n-1⋅⅕ for n ≥ 1 = 5.

 

[StoneTemplePython]

I have a picture of Fermat and he talks to me, so I can't take full credit.

I liked this quite a bit. It could also be quite useful for problem 6.

The expected number of rounds for the game to terminate = ∑n⋅prob game ends on nth round, n ∈ [1,8] (see post #60).
Prob game ends on nth round = prob "other" is rolled at the nth turn + prob game terminates by a win at the nth roll...

If she just keeps on flipping regardless of score the expected number of rounds = ∑n⋅⅘^n-1⋅⅕ for n ≥ 1 = 5.

This is right, and gives a quick and easy upper bound on the expected number of rounds with the stopping rule in place.

Solution to optional:
The expected number of rounds for the game to terminate = ∑n⋅prob game ends on nth round, n ∈ [1,8] (see post #60).
Prob game ends on nth round = prob "other" is rolled at the nth turn + prob game terminates by a win at the nth roll.
Let p = ⅖.

Round)
1) ⅕ + 0
2) (either a 1 or a 3) 2p⋅⅕ + 0
3) (either 1&1, or 1&3, or ...) 4p²⅕ + (3 3s) p³
4) (no 3s) p³ ⅕ + (1 3 & 2 1s) 3p³⅕ + (2 3s & 1 1) 3p³⅕ + (2 3s & a 1 then any) 6p⁴
5) (no 3s) p⁴⅕ + (1 3 & 3 1s) 4p⁴⅕ + (3 1s & 3 then 3) 4p⁵
6) (no 3s) p⁵⅕ + (1 3 & 4 1s) 5p⁵⅕ + (4 1s & 3 then any) 10p⁶ + (5 1s then 3) p⁶
7) (no 3s) p⁶⅕ + (6 1s then 3) p⁷
8) (no 3s) p⁷⅕ + (7 1s then any) 2p⁸
Now multiply the round by its total prob and add them up to get about 2.8 expected rounds.

The result here is awfully close but not quite right. I'd encourage you to write out the exact probabilities in the post.

For others benefit, I'd state it as having a counter vector

$\mathbf c = \begin{bmatrix} 1\\ 2\\ \vdots\\ 7\\ 8 \end{bmatrix}$

and a probability of terminating on that turn vector

$\mathbf p= \begin{bmatrix} ?\\ ?\\ \vdots\\ ?\\ ? \end{bmatrix}$

all entries in $\mathbf p$ would be real non-negative. And since we know that the game must terminate in one of those 8 rounds, and the termination times correspond to mutually exclusive events, the probability vector sums to one, i.e.

$\mathbf 1^T \mathbf p = \sum_{k=1}^8 p_k = 1$
- - - -
So, for the expected number of turns calculation, you have

$\text{expected time till termination} = \mathbf c^T \mathbf p = \sum_{k=1}^8 (c_k) p_k = \sum_{k=1}^8 (k)p_k$

- - - -
Interesting point: if the game starts at a certain other state -- not "s" though-- one gets $2.838$ as the expected rounds till termination. The expected time from "s", then, is strictly greater than this (inclusive of any rounding effects).

 

[Zafa Pi]

The result here is awfully close but not quite right. I'd encourage you to write out the exact probabilities in the post.

Change ⅕ to p/2.
1•p/2 = .2
2•2pp/2 = .32
3•(2p³ + p³ = 3p³) = .576
4•((p³ + 3p³ +3p³(corrected))p/2 + 6p⁴ = 9.5p⁴) = .9728
5•(5p⁴p/2 + 4p⁵ = 6.5p⁵) = .3328
6•(6p⁵p/2 + 11p⁶ = 14p⁶) = .344
7•(p⁶p/2 + p⁷ = 1.5p⁷) = .0172
8•(p⁷p/2 + 2p⁸ = 2.5p⁸) = .013

Adding the bolds = 2.7758 ≈ 2.8.
You're right there was an error at round 4, but to the nearest tenth it's still the same. Good looking out.
I waited for others to solve it, but think no one did because it was a bit messy and needed careful attention. The only real idea was the stopping rule.

 

[Zafa Pi]

not quite right

Wait, I had round 4 correct (except the first bold + shouldn't have been bold).
So where is the error?

 

[StoneTemplePython]

Wait, I had round 4 correct (except the first bold + shouldn't have been bold).
So where is the error?

let me try to transcribe the below -- I'm not concerned about minor rounding nits -- to the first or second decimal is fine.

(disclaimer: what I show below may look inconsistent on significant figures as I'm copying and pasting from python, etc.)

Change ⅕ to p/2.
1•p/2 = .2
2•2pp/2 = .32
3•(2p³ + p³ = 3p³) = .576
4•((p³ + 3p³ +3p³(corrected))p/2 + 6p⁴ = 9.5p⁴) = .9728
5•(5p⁴p/2 + 4p⁵ = 6.5p⁵) = .3328
6•(6p⁵p/2 + 11p⁶ = 14p⁶) = .344
7•(p⁶p/2 + p⁷ = 1.5p⁷) = .0172
8•(p⁷p/2 + 2p⁸ = 2.5p⁸) = .013

Adding the bolds = 2.7758 ≈ 2.8.
You're right there was an error at round 4, but to the nearest tenth it's still the same. Good looking out.
I waited for others to solve it, but think no one did because it was a bit messy and needed careful attention. The only real idea was the stopping rule.

$\mathbf v := \left[\begin{matrix}0.2\\0.32\\0.576\\0.9728\\0.3328\\0.344\\0.0172\\0.013\end{matrix}\right] = \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ 5\\ 6\\ 7\\ 8 \end{bmatrix} \circ \left[\begin{matrix}0.2\\0.16\\0.192\\0.2432\\0.06656\\0.0573333333333333\\0.00245714285714286\\0.001625\end{matrix}\right] = \mathbf c \circ \mathbf p$

where $\circ$ denotes element wise multiplication (Hadamard product).

I believe I got the transcription right but let me know if I missed something.
- - - -

going through it:

as you've said:
$\mathbf c^T \mathbf p = \text{sum}\big(\mathbf v\big) = \mathbf 1^T \mathbf v = 2.7758$

But
$\mathbf 1^T \mathbf p = \sum_{k=1}^8 p_k = 0.923175 \lt 1$which means you haven't included all paths that lead to termination. For avoidance of doubt, we know that all paths terminate with probability one. We know it for several reasons... you've already implicitly shown this by getting the upper bound case -- i.e. the expected time of 5, for the person who just loves coin tossing.

- - - -
I know of at least two other approaches besides enumeration that could get you there -- I tend to think they are easier though enumeration is a perfectly valid approach.

- - - -
edit:
your probabilities vector is off by just under 8 percentage points in total. This is entirely attributable to just one of the slots... i.e. you are correct in $7$ of the $8$ cases you've listed, but one of them is off by $\approx 8 \text{% points}$

 

[Zafa Pi]

which means you haven't included all paths that lead to termination.

OK,OK, you are correct. Nice observation.
My error was in round 4. I omitted a 3p⁴ = .0768 which, with exact calculations brings the total probability to 1.
The expected number of rounds then becomes 3.0831744.
So what is easier than enumeration? Run a zillion trials on a computer and take an average?
Thanks.

 

[StoneTemplePython]

OK,OK, you are correct. Nice observation.
My error was in round 4. I omitted a 3p⁴ = .0768 which, with exact calculations brings the total probability to 1.
The expected number of rounds then becomes 3.0831744.
So what is easier than enumeration? Run a zillion trials on a computer and take an average?
Thanks.

Simulations work well in practice, though they wouldn't count for credit here-- something more 'exact' is needed in the spirit of the problem and rules 1 and 4.

My preferred approach is to (a) think forward to reachable termination points i.e. $\{8,9,10,0\}$ -- given you have the stopping rule in place-- and these become your base case(s). Now apply backward induction.

This was my opaque reference earlier:

One technique that I particularly like would be familiar to Pascal, and, I think, Cauchy would approve.

though perhaps I could have mentioned Bellman and some others as well.

edit:
Strictly speaking I was thinking of the Pascal approach of drawing the tree and inducting backward in context of pricing this to be a 'fair game'. (Given that you have a stopping rule in place, this is not unlike a Problem of Points.)

The approach is quite flexible, though, and can be easily modified to get expected time till termination.

 

[Zafa Pi]

Simulations work well in practice, though they wouldn't count for credit here-- something more 'exact' is needed in the spirit of the problem and rules 1 and 4.

My preferred approach is to (a) think forward to reachable termination points i.e. $\{8,9,10,0\}$ -- given you have the stopping rule in place-- and these become your base case(s). Now apply backward induction.

This was my opaque reference earlier:
though perhaps I could have mentioned Bellman and some others as well.

edit:
Strictly speaking I was thinking of the Pascal approach of drawing the tree and inducting backward in context of pricing this to be a 'fair game'. (Given that you have a stopping rule in place, this is not unlike a Problem of Points.)

The approach is quite flexible, though, and can be easily modified to get expected time till termination.

If I understand you correctly it seems as though you will eventually end up with all of the same paths as I did, and your approach isn't any faster.

 

[StoneTemplePython]

If I understand you correctly it seems as though you will eventually end up with all of the same paths as I did, and your approach isn't any faster.

It depends, I suppose, on how you are generating your paths. The idea is to collapse things/ take advantage of overlapping subproblems. Think trellis lattice or recombining tree (maybe an abuse of language but a common term in finance).

The approach is a single linear scan through the states-- O(n) with bare minimal coefficient-- to get the answer to both the fair pricing and expected rounds till termination questions-- again, assuming you have a stopping rule in place. The approach also has the virtue of making it impossible to double count or omit paths.

(For what it's worth, another way of tackling the problem reduces to (sparse) matrix multiplication.)

I'm happy to post the approach at the end once this thread is closed out.

- - - -
Problem 6 is still open.

I'd be much obliged if someone tackles it. Depending on how one sets up the problem, it is either straightforward or an impossible task.

 

[fresh_42]

... and the $\mathbb{F}_8-$basis over $\mathbb{F}_2$ with its multiplication rules.

 

[Zafa Pi]

Problem 6 is still open.

I find #6 ambiguous. If an urn has 3 whites and 1 black what do you think is the probability of drawing 3 that are either all white or all black?

 

[Zafa Pi]

Problem 6 is still open.

I'd be much obliged if someone tackles it

The only way I can make a reasonable problem from the way it was posed is as follows:
The probability of getting all white or all black from urn 2 is prob all white + prob all black.
In that case it is impossible due to Fermat's Theorem and n ≥ 3.

That's what Fermat told me.

 

[StoneTemplePython]

The only way I can make a reasonable problem from the way it was posed is as follows:
The probability of getting all white or all black from urn 2 is prob all white + prob all black.
In that case it is impossible due to Fermat's Theorem and n ≥ 3.

That's what Fermat told me.

Can you expand on this a bit for others' benefit?

It's a mildly famous problem designed by E. C. Molina, to cast Fermat's Last Theorem as a probability problem.

 

[mfb]

There are some trivial solutions for (6).

If an urn has 3 whites and 1 black what do you think is the probability of drawing 3 that are either all white or all black?

1/4³ + (3/4)³. We draw with replacement.

In that case it is impossible due to Fermat's Theorem and n ≥ 3.

Huh?

 

[Zafa Pi]

Huh?

Let N be the number of balls in each urn, W the number of white balls in urn 1, b and w the number of black and white balls in urn 2, n > 2 the number drawn from each urn. With my interpretation in #73 of the problem we get:
(W/b+w)ⁿ = (b/b+w)ⁿ + (w/b+w)ⁿ.
Multiplying by (b+w)ⁿ we have Wⁿ = bⁿ + wⁿ which is impossible for n > 2 by Fermat's (Wiles') Theorem.

 

[mfb]

Ah. I interpreted "the probability that all white balls are drawn from the first urn" as probability that every white ball in the urn is drawn at least once.

 

[Zafa Pi]

Ah. I interpreted "the probability that all white balls are drawn from the first urn" as probability that every white ball in the urn is drawn at least once.

I think that the way the problem was formulated is problematic. I attempted to point that out to @StoneTemplePython in post #72, but received no response.
For example, If an urn contains 3 whites and one black, then what is the probability of drawing (with replacement) three balls such that they are either all white or all black? I think the only reasonable answer is ¾³, which = the probability of drawing three white balls. Thus urn 1 and urn 2 are the same is a solution.

Perhaps it should be said that the urns contain at least 3 (or n) of each color.

 

[StoneTemplePython]

I think that the way the problem was formulated is problematic. I attempted to point that out to @StoneTemplePython in post #72, but received no response.
For example, If an urn contains 3 whites and one black, then what is the probability of drawing (with replacement) three balls such that they are either all white or all black? I think the only reasonable answer is ¾³, which = the probability of drawing three white balls. Thus urn 1 and urn 2 are the same is a solution.

Perhaps it should be said that the urns contain at least 3 (or n) of each color.

This problem and its wording, setting aside one or two nits, is verbatim from Mosteller's Fifty Challenging Problems in Probability. It is the last problem in the book, of course numbered 50 56. (There are some bonus problems.)

People are free to ask questions to clarify, though posts #72 and #73, $\lt 3 \text{ hours }$ apart, both arrived while I was offline.

- - -
My read: Post #72 did not directly seek to clarify the wording of the question but instead said "what do you think...".

On the other hand, Post #73 was direct and had the answer. I responded to the most recent, accurate and direct post, #73.

- - -
n.b.

I also liked this:

That's what Fermat told me.

 

[mfb]

Post 73 doesn't address the interpretation question for urn 1. As you marked it as solved I guess the different wording for urn 1 doesn't mean anything. "It is impossible" is a strange solution to "Find the number of [...]".

With the other interpretation I could rule out 1 and 2 white balls in urn 1 for 3 and 4 drawings, but the problem gets much more difficult.

 

[Greg Bernhardt]

Just a couple more sub questions to be answered. Incredible works everyone!

 

[fresh_42]

First day open to all. Open: 1.b.) $\mathbb{F}_2-$ basis of $\mathbb{F}_8$ and its multiplication resp. addition structure.

 

[fresh_42]

Solution to 1.b)

From there determine a basis of $\mathbb{F}_8$ over $\mathbb{F}_2$ and write down its multiplication and addition laws.

This is actually the easiest part of all. Let's say we have the minimal polynomial $x^3+x+1=0\,$, and we assume a root $\xi \,$, i.e. an element which satisfies $\xi^3+\xi +1 =0$. Then
$$
x^3+x+1 = (x+\xi)(x+\xi^2)(x+\xi+\xi^2)
$$
and $\{1,\xi,\xi^2\}$ is a $\mathbb{F}_2$ basis of $\mathbb{F}_8$. The elements are thus
$$
\{0,1,\xi,\xi+1 = \xi^3,\xi^2,\xi^2+1=\xi^6,\xi^2+\xi=\xi^4,\xi^2+\xi+1=\xi^5\}
$$
which defines the multiplicative group generated by $\xi$ as well as the addition table.