- #1
theuniverse
- 55
- 0
Homework Statement
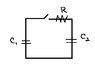
In the circuit below, C1 = 5 microfarads, C2 = 10 microfarads and R = 1000 ohms. Initially, the switch is open, C1 is charged to 20 volts, and C2 is uncharged. At time t=0 the switch is closed.
I think I managed to solve the first two but I have troubles with part (c):
(a) Calculate the voltage across C1 at a much later time.
(b) The energy stored in a charged capacitor is given by U = (CV^2)/2. Calculate the energy stored in C1 and C2 before and after closing the switch.
(c) Derive an expression for the power dissipated in R as a function of time for t>0.
Diagram:
|--------- switch -------- R------|
C1.........C2 [ignore the dots, they are just used for spacing)
|--------------------------------|
Thank you so much for your time,
Homework Equations
Q=CV
U = (CV^2)/2
P = I^2R
The Attempt at a Solution
a) Q initial=CV=(5)(20)=100 microF
when the switch is closed, the caps are in parallel which means that C total=15 microF
thus V=Q/C=100/15=6.7V
b) Before: U1 = (CV^2)/2=1000microJ
U2 = (CV^2)/2=0J
After: U1 = (CV^2)/2=111microJ
U2 = (CV^2)/2=222microJ
c) I know that total energy lost in resistor is 1000-333=667microJ and I think P = I^2R can be used somehow, but I need some help from here.
Thank you for your help!