Car gyroscopic effect problem/doubt

  • Thread starter Thread starter Shivanand
  • Start date Start date
  • Tags Tags
    Car
AI Thread Summary
In a vacuum, a car with a rotating flywheel cannot steer but will precess in the vertical plane when jets are fired, as the torque from the jets is perpendicular to the angular momentum vector. The minimum angular velocity needed to prevent steering motion is not specified, but the car's behavior is dictated by the flywheel's angular momentum. On a road, if the car is heavy enough to maintain contact and the flywheel is constrained from precessing, it will still feel "heavier" during a turn due to the dynamics of angular momentum. Even with a rigid setup and undeformable tires, resistance will still be perceived when turning. The discussion highlights the complexities of gyroscopic effects in vehicle dynamics.
Shivanand
Messages
9
Reaction score
0
Problem Statement

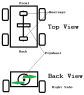
Suppose a car has mass M. It has a flywheel with axis running from front to back between left and right set of wheels. Let the flywheel have moment of inertia I and let it rotate clockwise at a constant angular velocity of w (omega). The flywheel shaft is held inside two bearings (front and back and it turns clockwise as seen from back of the car. Assume the shaft is massless (See the attached image).

1) If the car is not on road and in free space (vaccuum), if jets are fired from left-front and right-rear corner so that there is a torque tending to steer the car right, can the car steer or does it precess in vertical plane? If it steers, what is the minimum angular velocity of the flywheel to prevent the steering motion?

2)If the car is on road and it is heavy enough to stay in contact with road at all times, and it tries to take a right turn (steer right). The bearings are strong enough to prevent the flywheel from precessing in vertical plane. So the flywheel essentially is not allowed to precess. Will there be any resistance for the steering motion?



My attempt at solution

1) For the first problem I think the car cannot steer due to the jets and just precesses along with the flywheel in the vertical plane.

2) For the second problem I think no resistance is offered for the turn.

Am i right? If I am not could you please correct me? I would be glad to read your responses and ideas. :smile:
 

Attachments

  • Untitled.png
    Untitled.png
    2.2 KB · Views: 1,140
Physics news on Phys.org
1) Correct, it will just precess. The angular momentum vector points along the length of the car. The only source of torque are your two jets, and that torque is perpendicular to the angular momentum, so the angular momentum vector will rotate around axis perpendicular to the wheel axis. (I'm just using the later to denote direction. They have nothing to do with the physics.)

2) The car will seem "heavier" in the turn. It will also "try" to tilt forward or backwards, which you'll notice if there is suspension.
 
Hi,

Thanks for the quick reply..:approve:

If there is no suspension (or stiff suspension) and the car is rigid and does not allow any sort of rotation along precession axis, no precession takes place. Will the car still feel heavier to turn? I think that the angular momentum cannot be conserved by precessing and if the tyres are made of undeformable rigid material unaffected by the gyro effects, resistance will not be felt. Is it right? :confused:
 
It will still seem "heavier" on a turn.
 

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

I How to quantify gyroscopic precession torque?
Replies
34
Views
3K
B Does the Bernouli Effect Work On Cars?
Replies
8
Views
2K
Auto/Motor Design to 3D print RC car - Steering
Replies
8
Views
5K
Car in corner -- relative airflow
Replies
20
Views
3K
B Filming a passing road sign: speed vs bumpiness
Replies
16
Views
2K
Kids Ride on Toy Car Battery/Voltage
Replies
5
Views
3K
Can Weight Transfer Cause a Car to Stay in a Stuck Position?
Replies
14
Views
3K
Gyroscopic forces in a flywheel kers system
Replies
1
Views
2K
What is the direction of friction
Replies
1
Views
6K
Determine speed needed to cause rollover of car hitting ramp
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top