Car's maximum acceleration on a road is proportional to what?

[rudransh verma]

Homework Statement

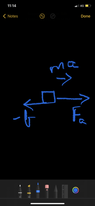
A car starts from rest to cover a distance s. mu is coefficient of friction between road and tyre. The minimum time in which the car covers the distance is proportional to :

Relevant Equations

$F=ma$

Since the car starts from rest it’s accelerating. So, $$F_a-f_k=ma$$
$$F_a-\mu mg=ma$$
$$\frac{F_a-\mu mg}m=a$$

Now from second eqn, $s=ut+\frac12at^2$
$$s=\frac12\frac{F_a-\mu mg}mt^2$$
$$\frac{2sm}{F_a-\mu mg}=t^2$$
$$\sqrt{\frac{2sm}{F_a-\mu mg}}=t$$

I don’t think I am getting any where!

 

[haruspex]

How well would a car accelerate if there were no friction between tyre and road?

 

[rudransh verma]

How well would a car accelerate if there were no friction between tyre and road?

It could not.

 

[jack action]

What is $F_a$?

The relevant equation is not $F=ma$, it is $\sum F = ma$ (Newton's 2nd law). Do a free body diagram. Do the summation of all forces present; don't create them out of thin air.

The friction force makes the ground push on the car and the car push on the ground. (Newton's 3rd law)

Once you'll figure this out, all the rest of your work will simplify very easily.

 

[rudransh verma]

What is Fa?

F applied!

The relevant equation is not F=ma, it is ∑F=ma (Newton's 2nd law). Do a free body diagram. Do the summation of all f

that’s what I did.

 

[bob012345]

F applied!

that’s what I did.

Please show us your free-body diagram.

 

[rudransh verma]

Please show us your free-body diagram.

Ok!

 

[kuruman]

I suppose the square object in the FBD is the tyre. What agent external to it exerts force $F_a$? In post #3 you correctly answered @haruspex's query that, if the contact were frictionless, the tyre would not accelerate. Well then, when the friction disappears, this $F_a$ must also disappear. How can that happen if the external agent exerts it away from the contact point?

 

[haruspex]

It could not.

So what is the role of that friction when a car accelerates? Which way does it act?
Remember, friction acts to oppose relative motion of surfaces in contact. If there were no friction, what would the relative motion of the tyre and road be?

 

[Steve4Physics]

@rudransh verma: you are standing still and start running.
1. What force accelerates you?
2. Assuming you have unlimited strength (!) is there any upper limit to your acceleration?

 

[jack action]

F applied!

that’s what I did.

Where does the applied force come from? I only see talk about friction in the question (thus I expect a friction force and nothing else).

 

[bob012345]

Ok!

Your free-body diagram is not yet correct. First, what kind of friction do you think is happening? Static or kinetic? Then, think about how the action of the motor ends up making the car accelerate. If you have a little wheel try and turn it against some surface with friction and feel what the wheel wants to do.

 

[rudransh verma]

suppose the square object in the FBD is the tyre. What agent external to it exerts force Fa?

Why have we started talking about tyres. In previous questions we talked about whole bodies as one. So why have we now started talking about their parts?

Your free-body diagram is not yet correct. First, what kind of friction do you think is happening? Static or kinetic?

of course kinetic.

 

[haruspex]

Why have we started talking about tyres. In previous questions we talked about whole bodies as one. So why have we now started talking about their parts?

That was rigid bodies. A car going along a road cannot be treated as a rigid body since the wheels rotate.

Edit: checking back I see that the issue here is that kuruman misinterpreted the FBD. Likely the square object was intended to represent the car as a whole, not just a tyre.

of course kinetic.

So the car is skidding?
I think we've been through this before: kinetic friction is when the surfaces in contact are in relative motion.

 

[rudransh verma]

That was rigid bodies. A car going along a road cannot be treated as a rigid body since the wheels rotate.

Ok!

So the car is skidding?
I think we've been through this before: kinetic friction is when the surfaces in contact are in relative motion.

yeah! (I am a slow learner) But I didn’t took the wheels of the car then. Now it’s wheels. It’s difficult to tell but I guess it’s static then.
Then, $$f_s=F_a (Force applied)$$
$$\mu_s mg=ma$$
$$\mu_s g=a$$
Then, $$s=\frac12at^2$$
$$\frac{2s}a=t^2$$
$$\frac{2s}{\mu_s g}=t^2$$
$t$ is proportional to $\sqrt{\frac1{\mu_s}}$

Seems right! My question is :
1. First of all this is not the question of car but of tyre, more accurately.
2.Net force is zero on tyre. $F_a=f_s$. But the car /tyre is accelerating which defies Newton’s second law!

 

[haruspex]

2.Net force is zero on tyre. $F_a=f_s$. But the car /tyre is accelerating which defies Newton’s second law!

You have not defined $F_a$, but used it as though it is the net horizontal force on the car, including the wheels.
If the wheels have mass m each and the car has mass M, $f_s=(M+4m)a$. The action/reaction between each wheel and thar car is $(M/4)a$, and the net force on the wheel is $ma$.

 

[rudransh verma]

You have not defined Fa, but used it as though it is the net horizontal force on the car, including the wheels.

It’s force applied and is not net.
Net is zero.

the wheels have mass m each and the car has mass M, fs=(M+4m)a.

$F_a= (M+4m)a$

 

[jbriggs444]

F applied!

that’s what I did.

For a car on the road as envisioned in this problem there is no applied force. There is just the car with its tires on the road.

When you press on the accelerator, it does not conjure up a team of horses to pull or a squad of men to push. Instead, it causes the tires to rotate. Friction between tires and road then becomes important.

 

[rudransh verma]

When you press on the accelerator, it does not conjure up a team of horses to pull or a squad of men to push. Instead, it causes the tires to rotate. Friction between tires and road then becomes important.

Can you explain what @haruspex said

The action/reaction between each wheel and thar car is (M/4)a, and the net force on the wheel is ma.

 

[jbriggs444]

Can you explain what @haruspex said

Perhaps. Let me first fetch the entire quotation.

You have not defined Fa, but used it as though it is the net horizontal force on the car, including the wheels.
If the wheels have mass $m$ each and the car has mass $M$, $f_s=(M+4m)a$. The action/reaction between each wheel and thar car is $(M/4)a$, and the net force on the wheel is $ma$.

@haruspex has done what I've repeatedly asked you to do. He has defined the variable names clearly before starting to write down equations with them.

We have five free bodies here. Four wheels plus a car. All share the same acceleration, $a$.

If we assume that this is a four-wheel drive vehicle with all four wheels contributing equally then each wheel will contribute 1/4 of the force required to propel the body of the car forward. By Newton's second law, the total forward force from wheels on car body must be $Ma$. By assumption, each wheel contributes 1/4 of that. That is, the force between each wheel and the body of the car will have magnitude $\frac{Ma}4$. Or $(M/4)a$ if you prefer.

[I prefer putting the parentheses around the net force ($Ma$) and dividing that into four parts rather than putting the parentheses around 1/4 of the car's mass and pretending that we have four unicycles accelerating together. But multiplication is associative so both interpretations give the same result]

The the net force (the sum of the rearward force from body of the car and the forward force from friction with the road) on each wheel must be $ma$ in order to satisfy Newton's second law.

 

[kuruman]

Perhaps it might be easier to consider first the one-wheel electric skateboard. The physics is the same. A car is just four of these hooked together with additional accoutrements piled on top and a centralized system for providing torque to two (or four) wheels.

 

[rudransh verma]

If we assume that this is a four-wheel drive vehicle with all four wheels contributing equally then each wheel will contribute 1/4 of the force required to propel the body of the car forward. By Newton's second law, the total forward force from wheels on car body must be Ma. By assumption, each wheel contributes 1/4 of that. That is, the force between each wheel and the body of the car will have magnitude Ma4. Or (M/4)a if you prefer.

That is a very nice explanation of car moving down the road.

The the net force (the sum of the rearward force from body of the car and the forward force from friction with the road) on each wheel must be ma in order to satisfy Newton's second law.

Yeah! It must be! But I don't understand rearward force from the body. Where does it come from?
Can you write in mathematical form?

 

[bob012345]

Perhaps it might be easier to consider first the one-wheel electric skateboard. The physics is the same. A car is just four of these hooked together with additional accoutrements piled on top and a centralized system for providing torque to two (or four) wheels.

View attachment 296544

Yes, It seems to me we are overcomplicating a very simple problem and it is not helping the OP understand the physics in my view.

 

[bob012345]

That is a very nice explanation of car moving down the road.

Yeah! It must be! But I don't understand rearward force from the body. Where does it come from?
Can you write in mathematical form?

This is simply an internal force between the wheels and the rest of the car. It is unnecessary to solve this problem. Consider the whole car as one object of mass $m$ to solve the problem for now and consider these extra details after you understand the physics fully to appreciate the bigger picture.

 

[jack action]

I don't understand rearward force from the body. Where does it come from?
Can you write in mathematical form?

You have to do the free body diagram for the wheel alone. You will have a torque applied (coming from the motor) and a reaction from the friction force. This should clarify what the direction of the friction force is.

Here's what it should look like (including the concept of rolling resistance, in green):

The torque applied is internal when you consider the whole car, thus why you don't have a "force applied" as you imagined. The force applied is the friction force, which is a reaction to the torque applied.

 

[bob012345]

You have to do the free body diagram for the wheel alone. You will have a torque applied (coming from the motor) and a reaction from the friction force. This should clarify what the direction of the friction force is.

Here's what it should look like (including the concept of rolling resistance, in green):

View attachment 296553​

The torque applied is internal when you consider the whole car, thus why you don't have a "force applied" as you imagined. The force applied is the friction force, which is a reaction to the torque applied.

Yes but even this is leaving out the force between the body of the car and the wheel which I am in favor of but we should not say this is the diagram of the wheel alone but that it represents the whole car in this problem. But the important point to the OP is what you said, that that it is the static friction force which is accelerating the car (we are ignoring rolling friction in this problem).

 

[hutchphd]

Newton's laws tell us two independent things:

1. The tire (friction) on the road causes a force on the road and the road pushes back with an equal and opposite force on the tire.
2. The tire will accelerate in a particular way because of that force: $\vec F=m\vec a$

Do not ever mix 1 and 2 in your brain. Never.

 

[rudransh verma]

But the important point to the OP is what you said, that that it is the static friction force which is accelerating the car (we are ignoring rolling friction in this problem).

If static friction is accelerating the car then my answer to the OP is wrong. It should be $f_s-F_a=ma$ where m is mass of tyre.

 

[Doc Al]

If static friction is accelerating the car then my answer to the OP is wrong. It should be $f_s-F_a=ma$ where m is mass of tyre.

I assume that the only force accelerating the car is static friction ($f_s$). There is no additional "applied force" ($F_a$) that I can see.

 

[rudransh verma]

There is no additional "applied force" (Fa) that I can see.

Why? What about the torque delivered by engine to the wheels?

 

[Doc Al]

Why? What about the torque delivered by engine to the wheels?

As others have pointed out, treat the car (including its tires and all other parts) as a single object. Treating the tires as separate objects only creates more work with no advantage.

 

[rudransh verma]

As others have pointed out, treat the car (including its tires and all other parts) as a single object. Treating the tires as separate objects only creates more work with no advantage.

But I was close to understanding what @jbriggs444 was telling about the distribution of force onto four wheels. I only didn’t understand the last line.
But now you are saying that treat it as a single body which is difficult to understand.
So can you explain me that last line only?

The the net force (the sum of the rearward force from body of the car and the forward force from friction with the road) on each wheel must be ma in order to satisfy Newton's second law.

 

[Doc Al]

But I was close to understanding what @jbriggs444 was telling but the distribution of force onto four wheels. I only didn’t understand the last line.
But now you are saying that treat it as a single body which is difficult to understand.
So can you explain me that last line only?

Sure. You could treat the tires separately. But the tires are connected to the rest of the car -- the tires push the car forward and the car pushes back on the tires. (Newton's third law!) If you want to call the force the car body exerts on a tire $F_a$, well now you have to solve for that!

But I cannot imagine why you'd do it that way. Treating the car as a whole, you have friction on the tires (which are part of the car) $f_s$ and the mass of the car. Finding the acceleration is one step away.

 

[Doc Al]

Treating the tires separately is overcomplicating a simple problem. (As another example: Say you need to calculate the acceleration of a block on a frictionless surface when you push with some force F. Do you break the block into pieces, like front half and back half? Well, you could -- you'd get the same answer with a bunch of unnecessary work.)

(And I don't think @jbriggs444 was recommending any such thing.)

 

[Doc Al]

So can you explain me that last line only?

Another way of saying the point @jbriggs444 was making: Take any piece of the car -- a tire, the steering wheel, whatever -- Newton's 2nd law must apply. The net force on that piece must equal $ma$, where $m$ is the mass of that piece.