Estanho
- 14
- 2
Hi,
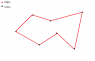
Suppose I have a data structure that models a polygon, by storing all the nodes of the given polygon, and their connections (i.e. edges).
I understand that sorting a set of nodes that may form a concave hull is ill-defined, as there could be many polygons that can be formed with those. But I'm asking about the case where the polygon is already defined by the edges. I'm attaching a drawing of such a polygon.
Is there an efficient and generic way to order the nodes of any such polygon, which may be concave, in ccw or cw?
Suppose I have a data structure that models a polygon, by storing all the nodes of the given polygon, and their connections (i.e. edges).
I understand that sorting a set of nodes that may form a concave hull is ill-defined, as there could be many polygons that can be formed with those. But I'm asking about the case where the polygon is already defined by the edges. I'm attaching a drawing of such a polygon.
Is there an efficient and generic way to order the nodes of any such polygon, which may be concave, in ccw or cw?