- #1
tuoni
- 61
- 0
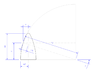
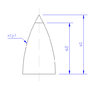
I am trying to find the centre of mass of a projectile nose. I profoundly suck at integration, but I have managed to work out area, and now I'm battling centre of mass. Am I doing this correctly? Is my final integral correct?
[tex]x = \sqrt{r_{1}^{2} - y^{2}} - (r_{1} - s_{2})[/tex]
[tex]\int{x \;\delta y} = \frac{y}{2}\sqrt{r_{1}^{2} - y^{2}} + \frac{r_{1}^{2}}{2} \cdot \tan^{-1} \left( \frac{y}{\sqrt{r_{1}^{2} - y^{2}}} \right) - y(r_{1} - s_{2})[/tex]
[tex]\delta V = 2 \pi \int{x \;\delta y}[/tex]
[tex]s_{"centre"} = \frac{\rho}{m} \int{x \;\delta V} = \frac{2 \pi\rho}{m} \int{x^{2} \;\delta y}[/tex]
[tex]x = \sqrt{r_{1}^{2} - y^{2}} - (r_{1} - s_{2})[/tex]
[tex]\int{x \;\delta y} = \frac{y}{2}\sqrt{r_{1}^{2} - y^{2}} + \frac{r_{1}^{2}}{2} \cdot \tan^{-1} \left( \frac{y}{\sqrt{r_{1}^{2} - y^{2}}} \right) - y(r_{1} - s_{2})[/tex]
[tex]\delta V = 2 \pi \int{x \;\delta y}[/tex]
[tex]s_{"centre"} = \frac{\rho}{m} \int{x \;\delta V} = \frac{2 \pi\rho}{m} \int{x^{2} \;\delta y}[/tex]