Centripetal Force - Banked Curve

AI Thread Summary
To determine the speed at which a 1000kg car must travel on a frictionless banked curve with a radius of 80m and a banking angle of 20 degrees, the centripetal force equation Fc = mv^2/r is applied. The discussion clarifies the use of perpendicular and parallel components of gravitational force, emphasizing that the perpendicular component (Fg(perp.) = mgcos(20)) is relevant for maintaining the car's circular motion. Participants explore the significance of these components in deriving the necessary equations for speed, specifically N*sin(20) = mv^2/r and N*cos(20) = mg. The solution involves solving these equations to find the required speed. Understanding the distinction between parallel and perpendicular forces is crucial for correctly applying the physics of banked curves.
Nicolaus
Messages
73
Reaction score
0

Homework Statement


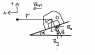
A 1000kg car travels around a frictionless banked curve having a radius of 80m. If the banking is 20 degrees to the horizontal, at which specific speed must the car travel to maintain a constant radius?


Homework Equations


Fc = mv^2/r
Fg(perp.) = mgcos(20)

The Attempt at a Solution


Would someone explain to me why we use the perp instead of the parallel angle on the incline? Is it because the car is traveling in the straight (toward the plane) direction along the banked curve?
 
Physics news on Phys.org
What do you mean by "parallel" and "perpendicular" angles?
 
I meant the force of gravity parallel and perp to the incline.
 
In the parallel and perpendicular coordinate axes, what is the reaction force and what is the acceleration?
 
Here's a diagram I made. N_x=m*v^2/r and N_y-G=0
we get two equations
N*sin20=mv^2/r and
N*cos20=mg
Then solve for v.
 

Attachments

  • diagram.png
    diagram.png
    2.2 KB · Views: 586
Last edited:
Thank you.
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Centripetal Force Banked Curves
Replies
12
Views
2K
Banked Road Physics Problem: Maximum Speed Calculation
Replies
5
Views
2K
Friction direction change in a inclined circular bend (car on a road)
Replies
11
Views
997
How do I draw a FBD for centripetal force
Replies
6
Views
4K
Solving Banked Curve Problem: Coefficient of Static Friction
Replies
6
Views
3K
What is the Needed Coefficient of Static Friction for a Car on a Banked Curve?
Replies
16
Views
2K
Centripetal Force Problem: Determine Vehicle Speed and Forces | 1988M1 Homework
Replies
4
Views
5K
Banked Curve-Determine smallest static coefficient of friction
Replies
9
Views
4K
Maximum Speed on a Banked Curve with Friction
Replies
19
Views
3K
Banked Turn: Navigating Car Dynamics on Curves
Replies
12
Views
3K

Hot Threads

Recent Insights

Back
Top