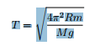Richer Su
- 4
- 0
Homework Statement
Refer to this pic https://www2.southeastern.edu/Academics/Faculty/rallain/plab193/page1/page37/page37.htmlor
I was wondering how increasing the mass at the bottom would influence the time taken for the object to complete 10 revolutions, my hypothesis was that it would decrease in an inverse ration manner of which I am still trying the find mathematically[/B]
Homework Equations
I understand that the centripetal force is F=mv^2/r
And the V=d/t = 2(pi)r/t
therefore the equation is
F=m(2(pi)r/t)^2 all divded by radius
The Attempt at a Solution
The
mass m1 will be the mass of a rubber stopper moving at a constant tangential speed of athttps://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.png the end of a nylon cord of length.https://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image004.png The centripetal force will be supplied by a mass thathttps://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image006.png is attached to the bottom of the nylon cord. See the above figure. Mass will include both the slotted mass and a hanger. The weight of this hanging mass is determined by the equation:https://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image008.png The weight of the hanging mass is the centripetal force applied to the mass https://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image010.png, keeping it in a horizontal circular orbit.
or
https://www.physicsforums.com/file:///C:/Users/RICHER~1/AppData/Local/Temp/msohtmlclip1/01/clip_image014.png
the final result in terms of T period was
See capture10000.Png
I'm not sure if this relationship is inverse manner and whether it is mathematically correct.
Any help would be appreciated!
Thanks