Centripetal force yo-yo problem

[gilboy64]

Hi,

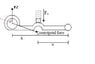
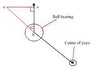
I am trying to find the speed it takes to open a yo-yo clutch, against a spring, to its maximum, the problem I am stuck on is whether you have to use F cos 90 - θ to get the centripetal force or if you have to do this in reverse eg. Fc = F / cos 90 - θ. I ask this because if you start with v using Fc = ω r you can find the centripetal force. You then can resolve it through cos 90 - θ to get the vertical component acting on the ball bearing. Then using moments you can model the clutch as a lever, and find the force exerted by the spring on the lever when it is opened to maximum. So, if you know the force exerted by the spring, working backwards, you should be able to find the speed. So, when you come to resolving the the force from the ball bearing, i think you should use the second one, Centripetal force = F / cos 90 - θ but i am not sure. Please help

thank you,
Gilmore

 

[gilboy64]

Hi, can anybody help?

 

[Doc Al]

I would be delighted to help, but I really don't know what you are asking. I have no idea what a "yo-yo clutch" is, and I can't relate your question to your diagram.

If you can describe it a bit more, that might help.

 

[gilboy64]

Its quite hard to explain without drawings, but basicly it is a lever that opens when the yo-yo is at a certain speed, there is a spring that stops it from opening until the speed is reached, and the force acting on the end of the lever (the ball bearing) is greater than the force exerted by the spring on the lever. I am tring to predict that speed, i have found the spring constant of the spring, and what force is exerted on the lever by the spring when the lever is open to its maximum. I have first used the moments on the lever to find the vertical force acting on the ball bearing. where x and y are distances.
x * force exerted by spring = y * force acting on ball bearing.
I know that the centripetal force acts directly from the center of the ball bearing into the center of the yo-yo, I also know that the centripetal force = mv2/r. So if I resolve the force on the ball bearing i can find the centripetal force and therefore the speed. But do I have to use centripetal force = F2 cos angle or (because the Fc is a 'real' force, and if I started with this force i definatly would cos angle) use Fc = F2 / Cos angle??
i hope this makes a little more sence

 

[Doc Al]

I'm still not quite getting it. (Maybe I need another cup of coffee?) But let me take a guess on what the problem is and make some comments. The forces on the ball bearing are two: the spring pulling it towards the center and the normal force of the yo-yo pushing it away from the center. The net force is: F_s - N. Since the yo-yo is spinning, the ball bearing is centripetally accelerated. Thus, Newton's 2nd law tells us that: F_s - N = m \omega^2 r. The ball bearing will separate from the yo-yo when the normal force = 0, which is at the speed where the spring is providing the full centripetal force: F_s = m \omega^2 r.

Let me know if I am getting closer to your question.

 

[Doc Al]

1 picture = 1000 words?

Ah... Now I think I see what you are talking about:
http://stuffo.howstuffworks.com/yo-yo3.htm

So to analyze the ball bearing from the reference frame of the yo-yo (an accelerating frame): You need to find the speed at which the centrifugal force on the bearing is enough to match the force of the spring on the lever. Then, yes, you need the component of the centrifugal force perpendicular to the lever arm. Equate the torque due to the spring to the torque due to the centrifugal force on the ball bearing.

Am I getting closer?

 

[gilboy64]

F_s = m \omega^2 r is the same as F_s = m v^2 / r, so if i know the Fs, I can find v. I know the force the spring is exerting on the lever, so using moments on the lever I can find the force acting vertically upwards on the ball bearing, right? So if I resolve this force so that it is now acting directly away from center of the yoyo it will be the same as the Fs, because the yoyo is spinning constanly the lever will be in equilibrium so the force = the same.
I have drawn one more picture, black arrows = the forces.
If I find angle (abc) I can resolve the vertical force (F) through this, my problem is to resolve this force through (abc) do i have to use F cos (abc) or F / cos (abc)??