Centripitalforce problem (hard)

[trondern]

Ok, I've been looking around for a answer for this , but haven't found one. So in hope for some help, ill post the problem here:


A pipe has the form as a half cylinder. On the top of the cylinder its placed a item that can slide frictionfree on the cylinder. The cylinder gets a microsmal puff, so the system starts. What angel does the radius make with the horizontal axis in the moment the item loses its contact with the cylindersurface?

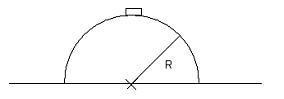
Any help solving this would be of great appreciaton from me :shy:

I've tried attacking this with finding an expression for the angle, but it failed. I am having problems really understanding what's causing the item to lose the surfacecontact with the cylinder. I am sure it has something to do with the speed of the item , combined with the angle for the position... I am really drawing a blank here.

 

[Chi Meson]

This is a classic problem that is in nearly every textbook I've looked through. I'll give you the standard hints:

You must assume that the object leaves the surface at an angle "theta."

What will the normal force on the object be at that moment?

What force (or componant thereof) provides the centripetal force at that moment?

In what way could you determine the speed of the object at that moment?

 

[trondern]

This is a classic problem that is in nearly every textbook I've looked through. I'll give you the standard hints:

You must assume that the object leaves the surface at an angle "theta."

What will the normal force on the object be at that moment?

What force (or componant thereof) provides the centripetal force at that moment?

In what way could you determine the speed of the object at that moment?

Thats what I've been trying to figgur out. There's no examples on it in my book, so its kinda hard to just see it happening.

I was thinking something like this, but unsure what to do with it.. hehe

mg cos(thetta+phi/2)..

seriously ..im drawing a blank here

 

[andrewchang]

if the object has just left the surface, can there be a normal force on it?

 

[trondern]

no, ok. Fn = 0. But I am still confused about what equations to use..

 

[Hootenanny]

You could use the conservation of energy theorm, or resolve forces radially giving you the normal reaction force. The choice is yours...

 

[trondern]

Those ..never used them before i think..

 

[Hootenanny]

How have you solved questions like this in the past?

 

[trondern]

I haven't solved any questions like this in the past. Thats why its kinda hard for me to get the picture here:)

 

[Chi Meson]

Here:

Up until the point "theta" the centripetal force is some force component minus the normal force. At "theta" cnetriipetal force is...

 

[trondern]

Up to thetta it is : sin (thetta) * mg - m*(v^2/R)

at thetta its : sin(thetta)*mg - 0 ?

This is hard:( What do i do with it afterwards?

 

[Chi Meson]

Up to thetta it is : sin (thetta) * mg - m*(v^2/R)

at thetta its : sin(thetta)*mg - 0 ?

This is hard:( What do i do with it afterwards?

This is the centripetal force at this point so it is equal to what other formula?

 

[trondern]

I have no clue...

 

[Doc Al]

I know that I'm just repeating, in slightly different words, what Chi Meson has already explained. Nonetheless...

There are only two forces acting on the object: its weight and the normal force of the surface. At the moment in question, when the object is just about to leave the surface, the normal force goes to zero: so the only force acting on the object (and the only force available to provide the centripetal force) is the weight.

You need to do two things:

(1) Apply Newton's 2nd law to forces in the radial direction, remembering that the object has a radial (centripetal) acceleration.

(2) Combine that with an expression relating angle with speed; you can derive one using conservation of energy.