jbunniii said:
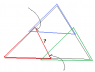
Here's my attempt to attach a picture of what I think has been established so far.
* ##A_1## contains the triangle defined by ##v_1##, ##x_{13}##, and ##x_{12}##, including vertices and edges
* ##A_2## contains the triangle defined by ##v_2##, ##x_{12}##, and ##x_{23}##, including vertices and edges
* ##A_3## contains the triangle defined by ##v_3##, ##x_{13}##, and ##x_{23}##, including vertices and edges
* the segment ##[v_3, x_{13})## contains only points of ##A_3##
* the segment ##[v_1, x_{13})## contains only points of ##A_1##
* the segment ##[v_1, x_{12})## contains only points of ##A_1##
* the segment ##[v_2, x_{12})## contains only points of ##A_2##
* the segment ##[v_2, x_{23})## contains only points of ##A_2##
* the segment ##[v_3, x_{23})## contains only points of ##A_3##
The attachment
Quoted to have it on the same page.
x
12 can be extended to a line segment on the edge where A
1 and A
2 intersect. Proof by contradiction: Suppose they would intersect at a single point only: Then their whole intersection is just this point (as they are convex), and x
12 would be the boundary of ##A_1 \cup A_2##. A
3 cannot include x
12, but would have to include points arbitrarily close to this -> it would not be closed, contradiction.
This allows to extend the triangles a bit, and ##A_1 \cap A_2## is a closed, convex set with non-empty interior. The same is true for the other two sides, of course.
Now consider the set ##((\partial A_1) \cap A_2) \cup ((\partial A_1) \cap A_3)## as subset of ##\partial A_1##, the boundary of A
1 (marked with the two arrows in the attachment). If the set is connected, we are done (the existence of a point in all A
i is then equivalent to the proof that a point x
12 exists).
If the set is not connected, there has to be some point in between which is at the boundary of A
1, but neither A
2 nor A
3 cover it (marked with a question mark). This is a boundary of ##A_1 \cup A_2 \cup A_3## in the interior of the triangle, which violates the condition that the union covers the whole triangle.
Alternatively: There is at least one point of ##\partial A_1 and \partial A_2## that is also in ##\partial (A_1 \cup A_2)## (not sure how to prove this). If this point is in A_3, we are done, otherwise it is a boundary of ##A_1 \cup A_2 \cup A_3## and we get the same contradiction as above.
I think we can replace the triangle by an arbitrary convex shape, where we divide the boundary in three regions that get the conditions the edges had in the original problem.