guyvsdcsniper
- 264
- 37
- Homework Statement
- 4.6 Friction / Dissipation. A volume of gas is contained in a wellinsulated
cylinder with a well- insulated piston head as depicted in Figure
4.4. The massless piston head may move but only by overcoming 0.2 newtons
of kinetic friction. A 50- g mass is placed on top of the piston head.
The piston head moves outward a distance of 25 cm. Ignore the pressure
exerted by the atmosphere.
(a) What is the amount of work performed by the gas during this
expansion?
(b) If we consider the gas, the cylinder, and the piston head to be part
of the system, what is the change in internal energy, ΔE, of the
system?
- Relevant Equations
- ΔE=Q+W
I believe I got the first part of this questions solved.
For part b, we are asked to find the change in internal energy.
We know ΔE=Q+W. The cylinder,gas and piston head are the system. The cylinder and piston head are well insulated, so there will be no head transfer, therefore Q=0.
So now we have ΔE=W. From part a, we found the work done to be .1725J.
By the equation above the change in energy is .1725J.
I don't know if that answer makes sense to me. The system is doing the work and by convention, work done by system is W<0.
But here I am getting a positive answer for overall change in energy.
Am I getting something wrong here?

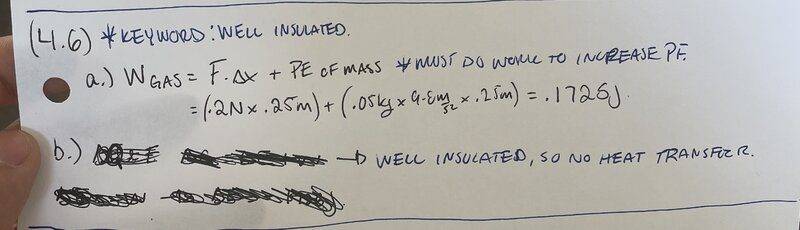
For part b, we are asked to find the change in internal energy.
We know ΔE=Q+W. The cylinder,gas and piston head are the system. The cylinder and piston head are well insulated, so there will be no head transfer, therefore Q=0.
So now we have ΔE=W. From part a, we found the work done to be .1725J.
By the equation above the change in energy is .1725J.
I don't know if that answer makes sense to me. The system is doing the work and by convention, work done by system is W<0.
But here I am getting a positive answer for overall change in energy.
Am I getting something wrong here?