Change of variables in summations

[Lajka]

Hi,

although this may sound trivial, I stumbled upon this problem while studying decimation process in digitial signal processing. I can't find anything on the web about some definition for the change of variables in sumations (as there is one for integrations), so maybe someone here could help me.

Consider the sum

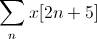
(the summation range is [-inf, +inf])

If I just do the substitution m=2n+5 and get this

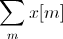
it wouldn't be right.

Decimation leads to irreversible changes, aka, I should still have the sum of elements x[1], x[3], x[5],..., but, somehow, I now have the sum of all elements of x[n] with this simple substitution.

So, I think the right answer would be

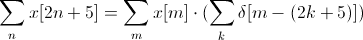
I did this ad-hoc, using logic. I was wondering if there is a proper definition for the change of variables in summations, which takes into the account the effects of decimation (which do not exist in continuous case of course)?

Thanks in advance :)

 

[Petr Mugver]

The problem is that, if n goes from minus to plus infinity, then m = 2n + 5 also goes from minus to plus infinity, but taking only odd values. So you could write

\sum_{n=-\infty}^{+\infty}x_{2n+5}=<br /> \sum_{m=-\infty}^{+\infty}x_{m}\frac{1-(-1)^{m+1}}{2}

This because the extra term I introduced is 0 for even m and 1 for odd m.

 

[Lajka]

Yeah, that does the same thing as the sequence of deltas, but I kinda like yours more :D

I guess there isn't a rule for this 'substitution' because it's a trivial matter, but I wanted to check it still.

Thank you for your response!