The disagreement boils down to what it means for two vectors to be equal. For example, if ##\vec u = (0, 0, 1)## and ##\vec v = (-1, 0, 1)##, in the absence of further information, no one would conclude that ##\vec u = \vec v##, because the coordinates are different. By the same token, no one would claim that T was the identity transformation if ##T(\vec u) = \vec v##, or equivalently, that ##A\vec u = \vec v## was the identity matrix, where A is the matrix representation of T.
On the other hand, if we agree that two different representations, in different bases, can refer to the same vector (your position), then what you say about a change-of-basis matrix does make sense. Although I took a year-long 400-level sequence in linear algebra while I was a grad student, the idea of a change-of-basis transformation/matrix being a sort of identity never came up. However, we did work with transformations and matrices using a notation similar to what you have been using. Of the several linear algebra textbooks I own, only one uses this notation: "Linear Algebra," by P.G. Kumpel and J.A. Thorpe.
In it they talk about the coordinates of a vector in terms of a basis B, using ##M_B(\vec v) = \begin{bmatrix}c_1\\ \vdots \\ c_n \end{bmatrix}##.
For the change-of-basis matrix of a transformation T, relative to the bases B and B', the notation is ##M^B_{~~B'}(T(\vec v))##. The columns of this matrix are ##\left[ M_B(\vec{ v_1}) \dots M_B(\vec{ v_n} )\right]##. Finally, the book I mentioned has a theorem about the representation of ##T(\vec v)## relative to a different basis B': ##M_{B'}(T(\vec v)) = M^B_{~~B'}(T) M_B (\vec v)##.
As an example, let ##E = \{\vec{e_1}, \vec{e_2}, \vec{e_3} \}## be the standard Euclidean basis for ##\mathbb R^3## and B be the basis ##\{\vec{e_1}, \vec{e_2}, \vec{b_3} \}##, with ##b_3 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}##, and T be the identity transformation relative to the standard basis, or I.
Per the formula above, ##M^E_{~~B}(I) = \begin{bmatrix} M_B(\vec{e_1}) M_B(\vec{e_2}) M_B(\vec{e_3}) (\end{bmatrix}##. Here each entry in the last matrix is a column vector.
This results in the matrix ##\begin{bmatrix}1 & 0 & -1\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}##.
This is the change-of-basis matrix, which changes a vector in E coordinates to its counterpart in B coordinates.
It's interesting to note that for this example ##\left(M^E_{~~B}(I)\right) \left( M^E_{~~B}(I)\right) = M^E_{~~B}(I)##, a result we would expect when multiplying an identity matrix by itself.
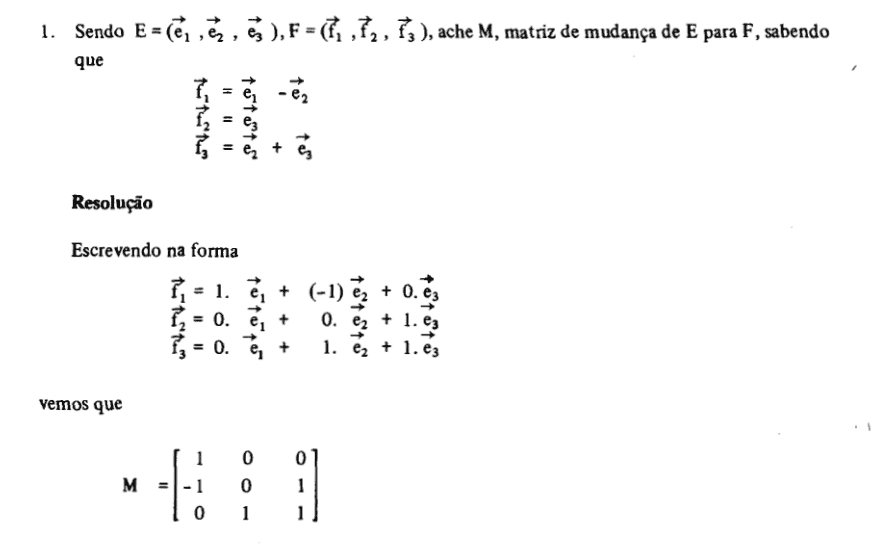
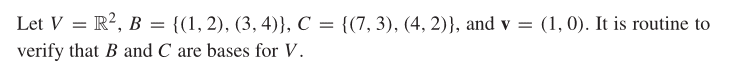
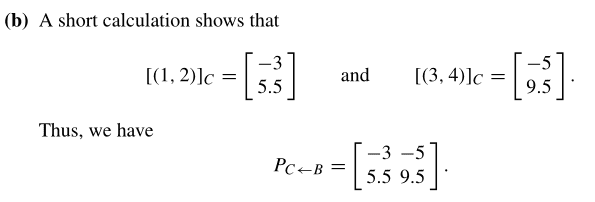 It ask the matrix B -> C, writing B in terms of C
It ask the matrix B -> C, writing B in terms of C
 XD
XD