Charged capacitor discharges to neutral cap energy losses?

[radaballer]

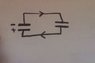
I want to calculate the total energy lost when a charged capacitor discharges to a neutral capacitor. It is my understanding that voltage will remain constant in the discharge, but current will decrease. What factors should be accounted for in any energy losses that would occur in this process?

 

[Dale]

Voltage will not remain constant. As written this circuit has no solution. You will want to include a resistor.

 

[gleem]

There is a solution. There is no energy loss for the ideal case. The energy is stored in the respective electric fields. The charge on the first capacitor when connected to the second is shared between the two. the voltage across both is the same since they are in parallel but this voltage is less than the initial voltage. Using Q=CV is all you need to determine v the voltage across the two connected capacitors. Using only Q = C1V with Q the total charge on the first capacitor and V its voltage and noting Q = q1 +q2 with q1 the charge on the first capacitor after connection and q2 ... you get that v the voltage on the connected capacitors becomes

v = V*(C1/(C1+C2))

from which you can show that the energy in the initial unconnected capacitor is equal to the energy of the connected capacitors.

I.e. ½ C1v² +½C2v² = ½C1V²

 

[stedwards]

The energy in a capacitor is $W=\frac{1}{2}CV^2$.
The voltage is $V=QC$.
$Q$ is the charge.

You can see that for two capacitors having the same capacitance, when connected in parallel, will equally share the charge. From the second equation, the voltage will drop in half. Each capacitor will then contain 1/4 of the energy of the charged capacitor. The lost energy is dissipated by the internal resistance of the capacitors.

 

[stedwards]

There is a solution. There is no energy loss for the ideal case. [...]
I.e. ½ C1v² +½C2v² = ½C1V²

I don't believe this is correct. Where did the missing energy go?

I'm afraid your equation really doesn't make any sense unless you identify whether each voltage is before or after current flows.

 

[gleem]

don't believe this is correct. Where did the missing energy go?

In my haste I made a boo boo and jumped to the wrong conclusion. mea culpa! blush blush

The lost energy is dissipated by the internal resistance of the capacitors.

However, there is no characteristic internal resistance for an ideal capacitor. . Ok, the missing energy had to go into the redistribution of the charge, I.e. work done in charging the second capacitor. which would be ½C2v². I think that take care of the missing energy

 

[tech99]

In my haste I made a boo boo and jumped to the wrong conclusion. mea culpa! blush blush

However, there is no characteristic internal resistance for an ideal capacitor. . Ok, the missing energy had to go into the redistribution of the charge, I.e. work done in charging the second capacitor. which would be ½C2v². I think that take care of the missing energy

I thought the capacitor problem was rather like the conservation of momentum when objects collide, when there is an energy loss.

 

[stedwards]

In my haste I made a boo boo and jumped to the wrong conclusion. mea culpa! blush blush

However, there is no characteristic internal resistance for an ideal capacitor. . Ok, the missing energy had to go into the redistribution of the charge, I.e. work done in charging the second capacitor. which would be ½C2v². I think that take care of the missing energy

The interesting thing about partially discharging one capacitor into another, is that the energy lose is independent of the size of the resistance between the two. I picked two equal sized capacitors, because the answer is easy; half the energy is lost in the resistor.

We can attempt to examine what happens when the two equal valued capacitors are ideal capacitors.

As the resistance goes to zero, the energy lose is unchanged. The current flow goes to infinity, the time constant goes to zero and the voltages reach equilibrium in zero time. The result really doesn't make any sense.

 

[gleem]

As the resistance goes to zero, the energy lose is unchanged. The current flow goes to infinity, the time constant goes to zero and the voltages reach equilibrium in zero time. The result really doesn't make any sense.

forget about the dynamics , details of the charge transfer.. Just consider the initial state and the requirements of the final state. Conservation of charge and the fact that the voltage across the connected capacitors is the same.

 

[stedwards]

forget about the dynamics , details of the charge transfer.. Just consider the initial state and the requirements of the final state. Conservation of charge and the fact that the voltage across the connected capacitors is the same.

Hm. I don't believe your getting this. If you think the final energy stored in both capacitors is equal to the initial stored energy, this would be wrong. You would need to correct your equations to identify initial and final voltages and charges.

 

[gleem]

Hm. I don't believe your getting this. If you think the final energy stored in both capacitors is equal to the initial stored energy, this would be wrong. You would need to correct your equations to identify initial and final voltages and charges.

I know that the energy on the initial capacitor is not conserved, I took care of that mistake in post 6.

Energy from the first capacitor is used to charge the second capacitor. You can show that the fraction of the initial energy used in moving the charge to capacitor 2 is C2/(C1+C2) which is equal to Q2/Q or the fraction of the total charge transferred to capacitor 2. BTW there is no intrinsic resistance for an ideal capacitor and it is negligible for a real capacitor.

Initial energy = Ei = ½C1V² =½ C1v² +½C2v² + work done in moving the charge to C2

where v = V(C1/(C!+C2))

Giving Ei = Ei(C1/(C1+C2)) + W

and W = (C2/(C1+C2)) = Q2/(Q1+Q2)) = Q2/Q

 

[Joe Ciancimino]

You will want to look into loss from the Q factor:

Quality Factor
https://en.wikipedia.org/wiki/Q_factor#Definition_of_the_quality_factor

 

[gleem]

Q factor is irrelevant, it applies to AC currents and depends on resistance which for this case is zero.

 

[nsaspook]

I remember this question from the last time. What happens if we slowly stretch the ideal capacitor plates area by a factor of two without changing the plate separation instead of adding another capacitor? The final energy is half the original value. Where is the missing energy?

 

[gleem]

Same place, in the work needed to distribute the charges over a larger area.

 

[stedwards]

I know that the energy on the initial capacitor is not conserved, I took care of that mistake in post 6.

Energy from the first capacitor is used to charge the second capacitor. You can show that the fraction of the initial energy used in moving the charge to capacitor 2 is C2/(C1+C2) which is equal to Q2/Q or the fraction of the total charge transferred to capacitor 2. BTW there is no intrinsic resistance for an ideal capacitor and it is negligible for a real capacitor.

Initial energy = Ei = ½C1V² =½ C1v² +½C2v² + work done in moving the charge to C2

where v = V(C1/(C!+C2))

Giving Ei = Ei(C1/(C1+C2)) + W

and W = (C2/(C1+C2)) = Q2/(Q1+Q2)) = Q2/Q

No, neither C2/(C1+C2) nor Q2/Q have units of energy, and you still haven't distinguished between initial and final voltages, energy, nor charge.Where both capacitors are equal in capacitance, $C$ and the initial voltage across $C_1$ is $V$. The initial voltage across $C_2$ is zero. $W$ is energy.

In general, $q=cv$, or $v=q/c$, and $w=c v^2$, or $w=q^2/c$.

$C_1=C$
$V_{1i}=V$
$C_2=C$
$V_{2i}=0$

$W_{1i}=\frac{1}{2} C_1 {V_{1i}}^2 = \frac{1}{2}CV^2$
$W_{2i}=\frac{1}{2} C_2 {V_{2i}}^2=0$

$W_{Total,i} = \frac{1}{2}CV^2+0$

Once equilibrium is achieved,

$V_{1f}= V_{2f}$.

$Q_{1f} = C V_{1f}$
$Q_{2f} = C V_{2f}=C V_{1f}$
or
$Q_{1f}=Q_{2f}$.

Charge is equally partitioned between both capacitors. Conservation of charge dictates that,
$Q_{1f}+Q_{2f} = Q_{1i}$.

Combining the last two equations,
$Q_{1f}=\frac{1}{2}Q_{1i}$
$Q_{2f}=\frac{1}{2}Q_{1i}$.

Using $v=q/c$,

$V_{1f}=\frac{1}{2}Q_{1i}/C = \frac{1}{2}Q/C = \frac{1}{2}V$
$V_{2f}=\frac{1}{2}Q_{1i}/C = \frac{1}{2}Q/C = \frac{1}{2}V$

$W_{1f} = \frac{1}{2}C(\frac{1}{2} V)^2 = \frac{1}{8}CV^2$
$W_{2f} = \frac{1}{2}C(\frac{1}{2} V)^2 = \frac{1}{8}CV^2$

$W_{Total,f}=\frac{1}{4}CV^2$

$W_{Total,f}=\frac{1}{2} W_{Ttotal,i}$
qed

If you wish to try this for unequal capacitors, that's up to you.

 

[gleem]

No, neither C2/(C1+C2) nor Q2/Q have units of energy, and you still haven't distinguished between initial and final voltages, energy, nor charge.

Oops I forgot the Ei I meant W = (C1/(C1+C2))⋅Ei = Q2⋅Ei/Q where C1 ≤ or ≥ C2

you could have just pointed out that omission.