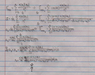degausser
- 3
- 0
Hello all,
I am new to PF; this is my first post. I am currently taking a physics class on electricity and magnetism.
I am trying to find an equation to calculate the final position of a charged particle p, given that there are n other particles.
Known:
+ initial (positions and velocities) and charges of all particles (including particle p)
+ mass of particle p
+ final time t
Find:
+ exact final position of particle p after the given time t
I tried working it out on paper, but I got stuck and don't know how to simplify it.
Does anyone know the equation for this?
I am new to PF; this is my first post. I am currently taking a physics class on electricity and magnetism.
I am trying to find an equation to calculate the final position of a charged particle p, given that there are n other particles.
Known:
+ initial (positions and velocities) and charges of all particles (including particle p)
+ mass of particle p
+ final time t
Find:
+ exact final position of particle p after the given time t
I tried working it out on paper, but I got stuck and don't know how to simplify it.
Does anyone know the equation for this?