Anabelle37
- 35
- 0
Homework Statement
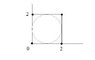
one duck is situated in each of the four corners of a 2mx2m square pen. suddenly, each duck begins to chase its anticlockwise neighbour. all the ducks travel at the same speed.
(a) by defining the origin of an x-y coordinate system in the bottom left hand corner of the paddock, show that the differential equation governing the path of the duck is dy/dx = (x-y)/(2-x-y); where (x,y) represents the position of the duck starting in the lower left corner.
what is the initial condition for the position of this duck.
The Attempt at a Solution
I have attached the file which shows the ducks in the four corners. I've also added a circle inside the square pen which represents the path of the ducks (not sure if this is right). I don't know where to go from here. I know I have to find expressions for dy/dt and dx/dt then use dy/dt=(dy/dx)*(dx/dt) to find dy/dx but I don't know how to find dx/dt and dy/dt?
Please help. It's revision for an exam!
Thanks