- #1
link223
- 70
- 12
- Homework Statement
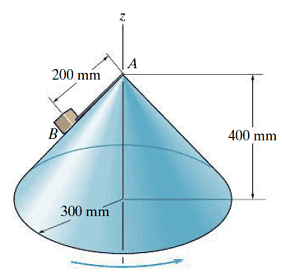
- The block B , having a mass of 0.2 kg, is attached to the vertex A of the right circular cone using a light cord. The cone is rotating at a constant angular rate about the z axis such that the block attains a speed of 0.5 m/s.
Part A
At this speed, determine the tension in the cord. Neglect the size of the block and the effect of friction.
Part B
At this speed, determine the reaction which the cone exerts on the block. Neglect the size of the block and the effect of friction.
- Relevant Equations
- newton
Haii, I don't understand why I need to choose my n-t components in the direction of a circular motion and can't just use them with the n-axis along the rope and the binormal perpendicular to the surface.