Circular motion - ball in a loop

[Pochen Liu]

Homework Statement

This question is referring to the classic ball in a loop question where it is dropped from a height and slides into a loop de loop.

Derive an expression in terms of theta the velocity of the ball at the time it loses contact with the track. Theta is measured from the horizontal at the height of the radius (Like the unit circle). And I am deeply struggling with this explanation

The ball will leave the rail when the rail reaction is zero. This happens when the centripetal force needed to travel around the loop is totally supplied by the component of the gravity force directed towards the centre of the motion.

I'm fine with the concept of working out the minimal velocity it needs so that the ball doesn't loose contact with the track v = sqrt(rg) because Fc and Fg are acting in the same direction

however how is the Fg acting along the radial part? It makes no sense to me as gravity should only act downwards in one direction not towards the center of the circle

Homework Equations

mg*sin(theta) = mv²/r - this is the equation I am struggling with, why is sin(theta) on the mg side

The Attempt at a Solution

My reasoning is that Fn vertical component when equal to Fg will start to fall, so if i draw a vector diagram and take out the vertical component of Fc/Fn

(mv²/r) * sin(theta) = mg

Can someone point out the fatal flaw in my intuition?

 

[kuruman]

My reasoning is that Fn vertical component when equal to Fg will start to fall ...

The ball will lose contact with the track when the normal force F_n becomes zero. The track can communicate to the ball that it's there only through the normal force.

 

[Pochen Liu]

The ball will lose contact with the track when the normal force F_n becomes zero. The track can communicate to the ball that it's there only through the normal force.

But how do we derive the part 'mg * sin(theta)' as normal force?

 

[kuruman]

You need to derive an expression for the normal force at some angle θ and see under what conditions F_n = 0. Draw a free body diagram.

 

[Pochen Liu]

You need to derive an expression for the normal force at some angle θ and see under what conditions F_n = 0. Draw a free body diagram.

Is this the correct diagram? (The question I am doing refers to theta from the horizontal btw)
If so, I don't understand why it is drawn like this, as in what is that 3rd vector I have labelled
I have drawn this diagram purely because I know this is the only way I can get mgsin(theta) to be along the radial direction

And in the second diagram as the ball moves towards the top of the circle theta gets smaller, but as the ball moves towards the top of the circle theta actually gets bigger.

I don't understand!

 

[kuruman]

Is this the correct diagram?

It would be the correct diagram if you omit the arrow that connects the tips of the normal force Fn and the weight Fg. That arrow does not represent the net force and, besides, the net force does not belong in a free body diagram. You are interested in the angle between Fn and Fg. How is it related to the angle x above the horizontal? Hint: In the diagram on the left draw a perpendicular line from the object to the horizontal dotted line. That gives you a right triangle.

 

[Pochen Liu]

It would be the correct diagram if you omit the arrow that connects the tips of the normal force Fn and the weight Fg. That arrow does not represent the net force and, besides, the net force does not belong in a free body diagram. You are interested in the angle between Fn and Fg. How is it related to the angle x above the horizontal? Hint: In the diagram on the left draw a perpendicular line from the object to the horizontal dotted line. That gives you a right triangle.

When I do that, I get this equation if I try relate x to Fc. I get this equation! Which was what I originally got and started my confusion

(mv^2/r)sin(theta) = mg

 

[kuruman]

When I do that, I get this equation if I try relate x to Fc. I get this equation! Which was what I originally got and started my confusion

Can you show me how you get this equation from the free body diagram? What is the component of the net force in the radial direction? What is that component equal to? Your expression in #7 does not have Fn in it.

 

[Pochen Liu]

Can you show me how you get this equation from the free body diagram? What is the component of the net force in the radial direction? What is that component equal to? Your expression in #7 does not have Fn in it.

This the diagram, if I understood your hint correctly.

 

[kuruman]

Yes, that's the diagram. What equation do you get from it when you apply Newton's Second Law in the radial direction?

 

[Pochen Liu]

Sin = O/H O = Fg H = Fn

Sin = Fg/Fn therefore

(mv^2/r) * sin(theta) = mg

which isn't correct, because it's supposed to be mg*sin(theta) = mv^2/r

 

[kuruman]

You are not applying Newton's Second Law. It has two sides.
1. The left hand side is the net force in the radial direction. What do you get when you add the two arrows in the diagram in the radial direction? There must be two terms because your diagram shows two forces.
2. The right hand side is mass times acceleration. What is that?

 

[Pochen Liu]

Im sorry I know this is painful for you.

The only things acting in the radial direction should only be Fn, because the centripetal force.
Gravity has nothing to do with it because it's only acting downwards. right?

So I get mv^2/r + 0 = mv^2/r

 

[kuruman]

So I get mv^2/r + 0 = mv^2/r

? mv²/r + 0 is always equal to mv²/r. Furthermore, mv²/r is the right hand side of the equation. One more time, what is the sum of the radial components of the two forces that you show in your diagram? There should be two non-zero terms. This is a general expression you are looking for. Get that first and then set Fn = 0 as a second step.

 

[Pochen Liu]

That's my confusion, I only see one force in the radial direction which is Fn. I honestly don't see how gravity has to do with anything in the radial direction. Hence the 0,
There are no components of a vector in a straight line? it's just downwards

 

[kuruman]

The radial direction is in general not horizontal and varies as the ball goes around the circle. Thus gravity has a component along it. What is that component? Draw a line from the tip of Fg perpendicular to Fn in your diagram and you will see.

 

[Pochen Liu]

Ok, so the straight line vector of gravity can be broken down into two vectors.

One that acts radially
One that acts tangentially?

So if I drop a ball there is in fact 2 forces acting on it from gravity alone that are perpendicular and cancel other than the vertical components

I can understand the tangential acceleration/deceleration because this is non-uniform circular motion.
So it's radially acceleration only because it's direction is changing?

 

[kuruman]

Ok, so the straight line vector of gravity can be broken down into two vectors.

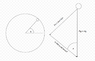
Start from here: Any vector can be broken into an infinity of pairs of vectors that are perpendicular to each other. For example, the acceleration of gravity $g$ can be the hypotenuse of a right triangle, $c=g$ the other two sides of which are $a=\beta g$ and $b=g\sqrt{1-\beta^2}$ where $0\leq \beta \leq 1$. You can easily verify that the Pythagorean theorem, $a^2+b^2=c^2$, holds for any value of $\beta$ and recognize $\beta$ and $\sqrt{1-\beta^2}$ as a sine and a cosine of some angle.

So in this case there is only one vector $\vec g$ that has fixed magnitude and direction, 9.8 m/s² straight down. As the ball goes around the circle, at the 12 o' clock and 6 o'clock positions it will have only a radial component and at the 3 o'clock and 9 o'clock positions it will have only a tangential component. It will have both kinds of component at intermediate positions on the circle. Note that the vector remains the same but the orientation of the coordinate systems that describes this vector changes continuously.

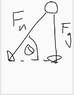
So if I drop a ball there is in fact 2 forces acting on it from gravity alone that are perpendicular and cancel other than the vertical components

If you drop a ball there, is only one force acting on it due to the Earth's influence. You can always view this as having two components in some arbitrary coordinate system `as described above, but it's not always a good idea to do so because it usually makes the mathematical analysis more complicated. When is it a good idea to do so? Answer: When, from the infinity of coordinate systems (infinity of $\beta$ values) you pick one that is germane to the problem at hand. Here you are interested in the normal force which is in the radial direction and so is the centripetal acceleration. Therefore it makes sense to pick the instantaneous radial direction as an axis and write Newton's Second Law in that direction.

can understand the tangential acceleration/deceleration because this is non-uniform circular motion.

Yes, as the ball goes around the circle there is a single net acceleration vector; its radial and tangential components change direction and magnitude continuously. Alternatively, you can view the net acceleration vector as the sum of two vectors: one is the acceleration of gravity and has fixed magnitude and direction and the other is the instantaneous normal force divided by the mass of the ball. The latter has changing magnitude but always points in the radial direction. As the ball goes around the circular track, the former component is always there while the latter component diminishes until it goes to zero. At that point the ball loses contact with the track, it is in free fall and undergoes projectile motion. That occurs at a critical value of $\beta$ defined above which is related to the cosine or sine of angle $x$ defined in your diagram. I will let you decide which one it is.

 

[haruspex]

Sin = O/H O = Fg H = Fn

Sin = Fg/Fn therefore

(mv^2/r) * sin(theta) = mg

which isn't correct, because it's supposed to be mg*sin(theta) = mv^2/r

As I explained to you elsewhere, centripetal force is not an applied force. It is a component of the resultant of all the applied forces; specifically, it is that component in the direction orthogonal to the velocity.
So, you look at all the applied forces, add them up and take the component of that which is at right angles to the velocity. That equals mv²/r.

Your equation was wrong because you took the vertical component of the centripetal force and equated that to the applied force. The applied force has another component, the one leading to tangential acceleration. So you could write mv²/r sin(θ) + m*(tangential acceleration) cos(θ) = mg, but that is not as useful since you do not know or care about the tangential acceleration. You would need to write also that since there is no horizontal force applied mv²/r cos(θ) = m*(tangential acceleration) sin(θ). You could then arrive at the right answer by combining the two equations.

 

[Dr Dr news]

The ball will leave the track when v = sqrt (g r cos theta). At that speed the radial force that the track exerts on the ball is zero.